Cox PH model을 활용하여, 설명 변수를 이용한 유저 생존 곡선을 그리고 수명을 측정한다.

문제 제기

이전 글, 유저 생존 곡선 그리기에서는 아주 간략하게 유저의 생존 곡선을 그리고, 수명을 측정하였다. 유저의 수명을 측정하게 되면, 어떤 유저는 오래 살고 어떤 유저는 그렇지 않은지 의문이 생긴다. 예를 들어, 다음과 같은 질문이 떠오른다.

광고를 통해서 유입된 유저와 그렇지 않은 유저는 수명 차이가 있을까? 있다면 얼마나 있을까?
가입 첫 번째 날의 서비스 사용 시간에 따라 유저의 수명에 차이가 있을까?
유료 구매 유저와 그렇지 않은 유저 사이에 수명 차이가 있을까?
유료 구매 횟수에 따라서 유저의 수명은 얼마나 영향을 받을까?

어떤 특성이 유저의 수명에 영향을 미치는지 알아보려면, 설명 변수를 추가하여 통계적 모형을 만든다. 가상의 데이터로 위의 질문에 대답해 본다.

데이터 소개

현실을 모방하여 아래와 같은 예시 데이터를 만든다. 인위적인 데이터를 사용하므로 분석 결과는 작위적이며 실제 현상과 다를 수 있다. 다만, 상식에 부합하는 범위 내에서 데이터를 생성하였다.

cid: client id
t: time to churn event(days)
churn: churned or not(0: active, 1: churned)
x1: marketing channel(0: by self, 1: by promotion)
x2: duration time of the first day(minutes)
x3: the number of purchase

데이터 모양은 아래와 같다.

cid    t    churn    x1    x2    x3
A      8    1        0     121   3
B      7    0        1     35    1
C      6    0        1     12    0
...

유저 생존 곡선 그리기의 예제 데이터와 다른 점은 x1, x2, x3라는 설명 변수가 추가되었다는 점이다. 기존 글에서는 그룹 사이의 생존 곡선을 따로 그려서 비교하는 방법에 그쳤다. 이 글에서는 세 개의 설명 변수를 이용해 통계 모형을 만들어 유저의 수명을 설명한다.

모형 소개

변수를 추가하여 수명을 설명하기 위해서 The Cox Proportional Hazard Model을 사용한다. 먼저 hazard function을 이해하고, Cox PH model에 대해서 설명한다.

위험률 함수(hazard function)

hazard란 위험률을 의미하는데, 어느 시점에 유저가 이탈할 가능성이 높은지 평가하는 비율이다. 위험률 함수는 아래와 같이 정의한다.

\[h(t) = \lim_{\Delta t \to 0} \frac{P(t \le T \lt t + \Delta t \,\lvert\, T \ge t)}{\Delta t}\]

$T$: random variable for user’s survival time
$t$: specific value for random variable $T$.

위의 수식을 직관적으로 이해하면 ‘특정 시점 $t$에서의 순간 위험률’이다.

$P(t \le T \lt t + \Delta t \,\lvert\, T \ge t)$은 t시점까지 살아 남은 유저($T \ge t$)가 다음 $\Delta t$ 시간 안에 죽을($t \le T \lt t + \Delta t$) 확률을 의미한다. ‘$t$시점까지 살아남은 유저’라는 조건 하에서 확률을 계산하므로 조건부 확률이다. 조건부 확률에 대해서는 유저가 접속할 확률 계산하기의 설명을 참고한다. 이 확률 값을 시간 $\Delta t$로 나누면 ‘단위 시간 당 죽을 가능성’이 된다. $\Delta t$가 1보다 작은 경우도 있으므로, 이 숫자는 더 이상 확률이 아니라 비율이 된다. 즉, 1보다 큰 수를 가질 수 있다.

\[0 \le \frac{P(t \le T \lt t + \Delta t \,\lvert\, T \ge t)}{\Delta t} \lt \infty\]

이 비율 함수에 $\Delta t \to 0$의 극한 개념을 적용하면, 특정 시점 $t$에서의 순간(instantaneous) 위험률 함수를 도출할 수 있다. 이것이 hazard function, $h(t)$다.

위험률 함수는 생존 함수와 밀접한 관련이 있는데, 둘 중에 하나만 알면 다른 하나의 함수를 알 수 있다.

\[h(t) = \lambda \iff S(t)=e^{-\lambda t}\]

위험률 함수 예시

생존 함수는 유저가 얼마나 오래 살아 남았는가를 나타내는 반면에, 위험률 함수는 특정 시점에서 죽을 가능성을 나타낸다. 예를 들어, 시간에 따른 시스템의 위험 곡선을 그려보면 아래 그림의 파란 색 곡선과 같다. 초기에는 시스템이 실패할 가능성이 매우 높다가, 안정기가 되어서 위험률은 낮아진다. 그러다가 다시 시스템이 낡아서 실패 가능성은 높아진다.

Bathtub_curve

그림 출처: wikipedia

이러한 현상은 아래 그림처럼 사람의 사망률에서도 유사하게 나타나는데, 영유아기와 노년기에 사망률이 높기 때문이다.

USGompertzCurve

그림 출처: wikipedia

이와 마찬가지로, 어떤 서비스를 이용하는 유저의 이탈 가능성을 위험률 함수로 표현할 수 있다. 또한 위험률 함수는 생존 분석(survival analysis)에서 통계 모형을 나타내는 용도로 쓰인다. 그 중 대표적인 모형이 Cox PH model이다.

The Cox PH model

The Cox Proportional Hazard Model은 설명 변수를 포함하여, hazard function에 대해 아래와 같은 통계적 모형을 도출한다. 예시 데이터에서는 설명 변수가 $X_1$, $X_2$, $X_3$ 뿐이므로 3개의 설명 변수만을 표기하였으나, 이는 확장 가능하다.

\[h(t, X_1, X_2, X_3) = h_0(t)exp(\beta_1 X_1 + \beta_2 X_2 + \beta_3 X_3)\]

$h_{0}$: baseline hazard function (case of $X_1 = 0, X_2 = 0, X_3 = 0$)

데이터가 주어지면 위의 모형에서 $\beta_1$, $\beta_2$, $\beta_3$를 추정하여 모형을 완성시킨다. R에서는 survival 패키지의 coxph 함수를 사용하여 모형을 만들 수 있다.

> coxph.fit <- coxph(Surv(t, churn) ~ X1 + X2 + X3, data=test)

실제로 데이터를 이용하여 도출한 모형은 아래와 같다.

\[h(t, X_1, X_2, X_3) = h_0(t)exp(1.08452 X_1 -0.03050 X_2 -0.07374 X_3)\]

> summary(coxph.fit)

Call:
coxph(formula = Surv(time, churn) ~ promo + dt + purchase, data = surv_df)

  n= 1000, number of events= 818

             coef exp(coef) se(coef)       z Pr(>|z|)
promo     1.08452   2.95802  0.07410  14.636  < 2e-16 ***
dt       -0.03050   0.96996  0.00128 -23.834  < 2e-16 ***
purchase -0.07374   0.92891  0.01929  -3.823 0.000132 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

         exp(coef) exp(-coef) lower .95 upper .95
promo       2.9580     0.3381    2.5582    3.4204
dt          0.9700     1.0310    0.9675    0.9724
purchase    0.9289     1.0765    0.8944    0.9647

모형 해석

컴퓨터를 사용하면 모형의 결과는 매우 쉽게 구할 수 있다. 아래와 같은 과정을 거쳐 이 모형이 어떤 의미를 갖는지 알아본다.

Hazard Ratio

$\beta_1$, $\beta_2$, $\beta_3$의 의미는 무엇일까? $\beta_1$에 대해서 알아보자.

$\beta_1$은 $X_1$의 계수이므로, 당연히 $X_1$ 변수와 관계가 있다. 광고를 통해서 유입된 유저는 $X_1 = 1$이고, 자발적으로 유입된 유저는 $X_1 = 0$이다. 따라서 두 그룹에 대한 위험률 함수는 각각 아래와 같다.

\[h(t, X_1 = 1, X_2, X_3) = h_0(t)exp(\beta_1 \times 1 + \beta_2 X_2 + \beta_3 X_3)\] \[h(t, X_1 = 0, X_2, X_3) = h_0(t)exp(\beta_1 \times 0 + \beta_2 X_2 + \beta_3 X_3)\]

자발적으로 유입된 유저와 광고로 유입된 유저의 위험률 함수를 나누면 이를 위험률 비, hazard ratio라고 한다.

\[\text{hazard ratio} = \frac{h(t, X_1 = 1, X_2, X_3)}{h(t, X_1 = 0, X_2, X_3)} = exp(\beta_1) = 2.958\]

이를 직관적으로 해석하면, 광고를 통해 들어온 유저는 자발적으로 유입된 유저에 비해서 죽을(chunred) 위험성이 2.96배 높다는 의미다. 나머지 $\beta_2$와 $\beta_3$도 같은 식으로 해석이 가능하다. $h_0(t)$는 ratio를 계산하는 과정에서 소거되므로, $\beta$ 값을 해석하는데 아무런 영향을 주지 않는다. 또한 시간($t$)은 모형에서 $h_0(t)$ 항에만 존재하는데, 이 때문에 설명 변수와 시간은 서로 영향을 주지 않는다.

달리 말하면, the cox PH model은 시간이 흘러도 위험률 사이의 비율은 변하지 않는 모형이다. 시간이 흐르면서 위험률은 달라질 수 있지만, 설명 변수 X에 따라 달라지는 각 그룹 사이의 위험률 비(hazard ratio)는 변하지 않는다. 데이터가 이러한 가정을 만족하지 않는다면 다른 모형을 사용한다.

Adjusted Survival Curves

이렇게 얻은 모형으로 특정 설명 변수를 갖는 유저의 생존 곡선을 그릴 수 있다. 만약, 광고를 통해서 유입되었고, 첫번째 날의 접속 시간이 100분이면서, 구매 횟수가 3회인 유저의 생존 곡선이 궁금하다면 위에서 도출한 모형으로 이를 쉽게 나타낼 수 있다.

> d.coxph <- survfit(coxph.fit, c(promo=1, dt=100, purchase=3)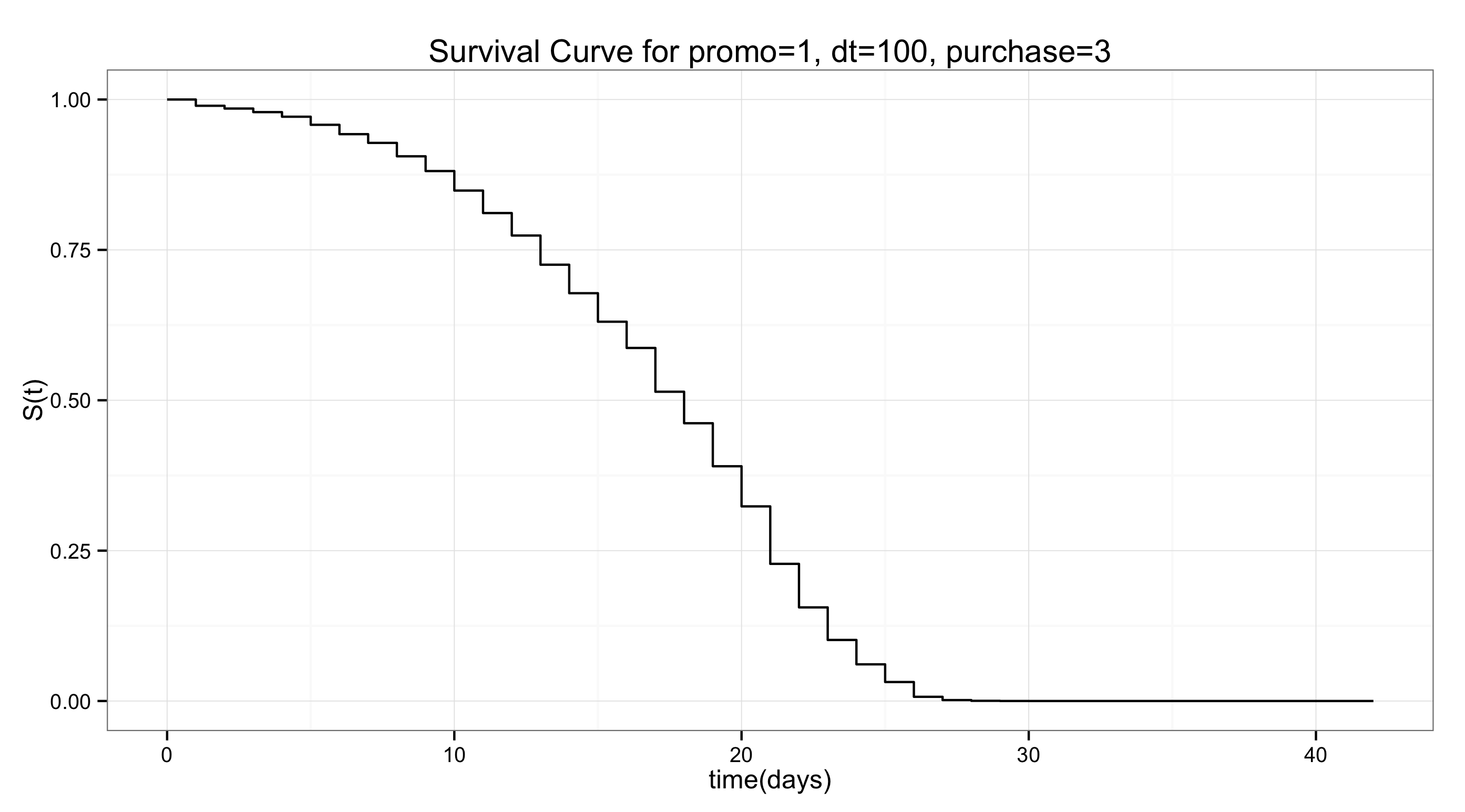

adjuted.survival.curve

이는 해당 조건을 만족하는 유저 한 명이 언제 죽을 것인가에 대한 대답이 아니다. 동일 조건의 유저들로 구성된 그룹이 있다면, 이 유저들이 죽는데 어느 정도의 시간들이 걸리는지를 추정한 것이다.

이는 물론 해당 조건을 만족하는 유저들의 실제 데이터와 차이가 있을 수 있다. 그러나 데이터를 근거로 추정한 모형에 바탕을 두므로 상당히 신뢰할 수 있다. 특히, 막연한 추측이나 큰 고민없이 계산한 기술(descriptive) 통계에 비해서 의사 결정의 근거로 활용하기에 더 유용하다.

promo=1, dt=100, purchase=3 이라는 조건과는 다른 유저의 생존 곡선이 필요하다면, 모형을 이용해서 다시 계산한다. 예를 들어, 기존과 같은 조건에서 dt=180인 유저의 생존 곡선은 아래와 같이 구할 수 있다.

> d.coxph <- survfit(coxph.fit, c(promo=1, dt=180, purchase=3)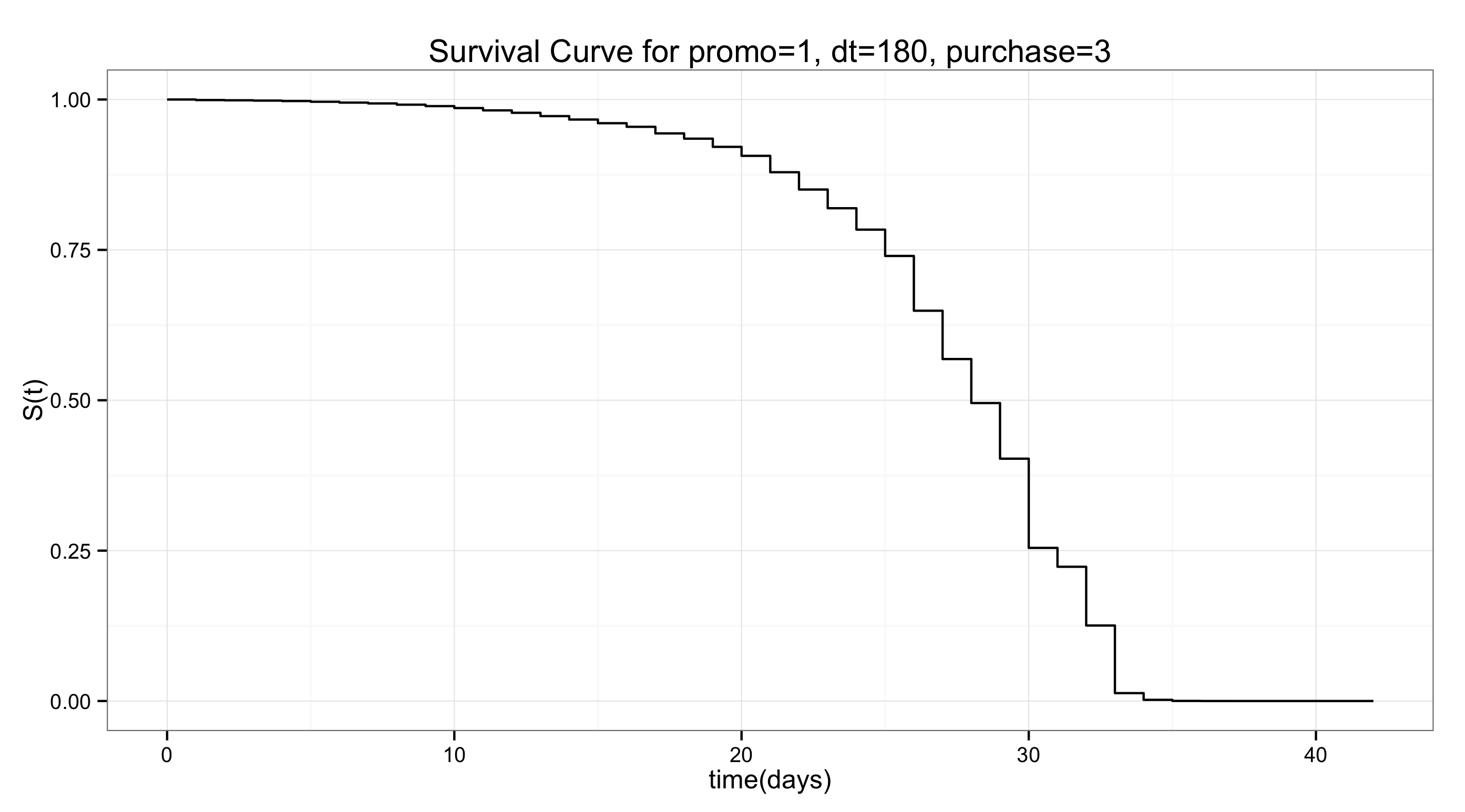

adjuted.survival.curve2

광고를 통해 유입되었고, 구매 빈도가 3인 고객의 경우 DT에 따라서 생존 시간이 위와 같은 차이를 보인다. 즉, 초반 서비스 사용 시간이 길수록 고객이 더 오래 생존할 가능성이 높다.

결과

여러 개의 설명 변수로 유저의 생존 곡선을 추정할 수 있다. 특히, 각 설명 변수에 의해서 생존 곡선이 어떻게 달라지는지 수치로 확인할 수 있다는 장점이 있다. 만약, 광고에 대한 성과를 측정하고 싶다면 광고로 유입된 유저들의 생존 기간에 일별 ARPU 등을 곱하여 예상 매출을 구할 수 있다. 광고 비용이 해당 매출을 넘지 못한다면, 그 광고는 손실이 발생하므로 필요없다.

첫 방문에서 유저가 서비스를 사용한 시간에 따라 생존 시간의 차이가 크다면, 첫 방문의 유저 경험에 더 많은 관심을 기울이는 것이 좋다. 물론 인과관계를 확인한 것은 아니지만, 인관계가 있을 가능성은 충분하며, 이를 계량화시켜서 평가하고 실행에 옮기는 것은 좋은 방법이다.

이외에도 측정 가능하고, 관심 대상이 될 수 있는 설명 변수를 추가하여 분석하면, 다음 실행안을 도출할 수 있는 단서를 얻을 수 있다. 이미 기록하고 있지만, 제대로 활용하지 못하고 있는 데이터만으로도 똑똑한 방법을 사용하면 그 가치는 훨씬 커진다.

문제점

Cox PH model은 설명 변수가 시간과 독립적인 관계를 갖는다고 가정하나, 이는 현실에서 맞지 않는 경우가 많다. 시간이 흐르면서 설명 변수의 값은 변화하는 경우가 많기 때문에, 이를 고려하지 않으면 제대로된 모형을 만들기 어렵다. 따라서 가정이 맞는지 점검하고, 가정을 만족하지 않는 경우에 사용할 또 다른 모형을 준비해야 한다. 이는 다른 글에서 다루도록 한다.

시간 축을 다양하게 설정이 가능한데, 이러한 경우 left-truncated data에 대한 고민이 필요하다. 다른 시간 축을 사용하면서 생기는 문제에 대해서는 다른 글에서 다루기로 한다.

이전 글: 유저 생존 곡선 그리기

참고

John P. Klein, Melvin L. Moeschberger(1997), Survival Analysis: Techniques for Censored and Truncated Data, Springer

-[|]- Box and Whisker

설명 변수를 이용하여 유저 생존 곡선 그리기