컴퓨터를 이용해서 시뮬레이션을 하거나, 특정 확률 분포 가정 하에서 테스팅을 하는 경우에 난수 생성기가 필요하다. 대부분의 프로그래밍 언어는 특정 분포를 따르는 난수 생성 함수를 제공하지만, 모든 분포에 대해서 제공하지는 않는다. 필요한 확률 분포를 따르는 난수 생성기가 없을 때, 이를 쉽게 구현하는 방법에 대해서 설명한다.

다양한 무작위성

세상에서 실제 동작할 코드를 작성하다보면, 정말 세상에 내놓았을 때 잘 작동할지 궁금하다. 이를 미리 증명해보기 위해서 시뮬레이션을 하거나 단위 테스트를 만들어 확인한다. 문제는 세상의 불확실성을 모사하는 것이 어렵다는 점인데, 보통 난수를 생성해서 복잡한 세상을 흉내낸다.

특정 문제를 해결하는 과정을 거치면서, 프로그램이 작동해야 하는 세상도 상당히 구체적으로 정의된다. 이때, 단순한 무작위성이 아니라 특정 문제에 내포된 무작위성이 필요하다. 세상에는 서로 성격이 다른 무작위성이 존재하는데, 통계학자들이 이런 무작위성을 잘 정리하여 특정 확률 분포들로 정의해 두었다. 문제가 충분히 구체적이면, 구체적으로 어떤 무작위성을 활용해서 프로그램을 테스트해야 할지 정할 수 있다.

기본 난수 생성기

가장 기본적인 난수 생성기는 균등분포(uniform dist.) 난수 생성기다. 보통 난수 생성기라고 하면 이를 말한다. 기본적으로 0부터 1사이의 값을 무작위로 생성한다. 거의 모든 프로그래밍 언어는 어떤 형태로든 기본 난수 생성기를 제공한다. 균등분포 난수 생성기가 없다면, 다른 분포를 따르는 난수 생성기는 만들 수 없다. 반대로 균등분포 난수 생성기만 있으면 어떤 분포를 따르는 난수 생성기든 모두 만들 수 있다.

균등 분포의 보편성

확률 밀도 함수(pdf)의 특징 중 하나는 모두 적분해서 1이라는 점이다. 이는 확률의 범위가 항상 0과 1사이라는 이야기와 같다. 기본 난수 생성기의 난수 생성 범위가 0과 1사이라는 점을 이용하면 무언가 할 수 있을 것 같다.

특정 확률 분포를 따르는 확률 변수 $X$에 대해서 난수를 추출하고 싶다고 하자. 확률 변수 $X$의 누적 분포 함수(CDF) $F(x)$의 역함수 $F^{-1}$을 알 수 있다면 기본 난수 생성기를 이용하여 확률 변수 $X$에 대한 난수 생성기를 만들 수 있다. 기본 난수 생성기를 확률 변수 $U$로 정의하면 이 확률 변수는 $Unif(0, 1)$을 따르며, 아래와 같이 정리할 수 있다.

\[X = F^{-1}(U)\]

쉽게 정리하자면, 확률 변수 $X$의 난수는 자기 자신의 누적 분포 함수의 역함수에 기본 난수를 대입하여 얻을 수 있다. 확률 변수 $X$가 어떤 확률 분포를 따르든 상관 없이 균등 분포를 이용할 수 있으므로 이를 균등 분포의 보편성(Universality of Uniform)이라고 부른다. 즉, 균등 분포만 있으면 다른 모든 분포를 만들어낼 수 있다. 혹은 누적 분포 함수의 역함수 변환을 통한 난수 추출 방법이기 때문에 Inverse transform sampling이라고도 부른다.

여러 가지 난수 생성기

로지스틱 분포를 따르는 난수 생성기

예를 들어, 로지스틱 분포를 따르는 난수 생성기를 만들고 싶다. 불행히도 우리가 이용하는 프로그래밍 언어에는 로지스틱 난수 생성기가 없다고 가정하자. 물론 기본 난수 생성기는 있으므로 이를 사용한다. 로지스틱 누적 분포 함수는 아래와 같다.

\[F(x) = \frac{e^{x}}{1 + e^{x}}\]

기본 난수 생성기를 확률 변수 $U$로 표현하면, $F^{-1}$에 $U$를 대입하여 로지스틱 함수를 따르는 확률 변수를 생성할 수 있다.

\[F^{-1}(U) = log(\frac{U}{1 - U}) \sim \text{Logistic}\]

위 식을 코드로 옮기면 아래와 같다. 기본 난수 생성기에서 추출한 균등 분포 자료를 로지스틱 누적 분포 함수의 역함수에 대입하면 로지스틱 난수가 된다.

# python3
import math
import random

def inv_logistic_cdf(u):
    return math.log(u / (1 - u))

# random numbers of Unif(0, 1)
random_numbers = [random.random() for _ in range(10000)]

# random numbers of Logistic Dist. through the inverse transform
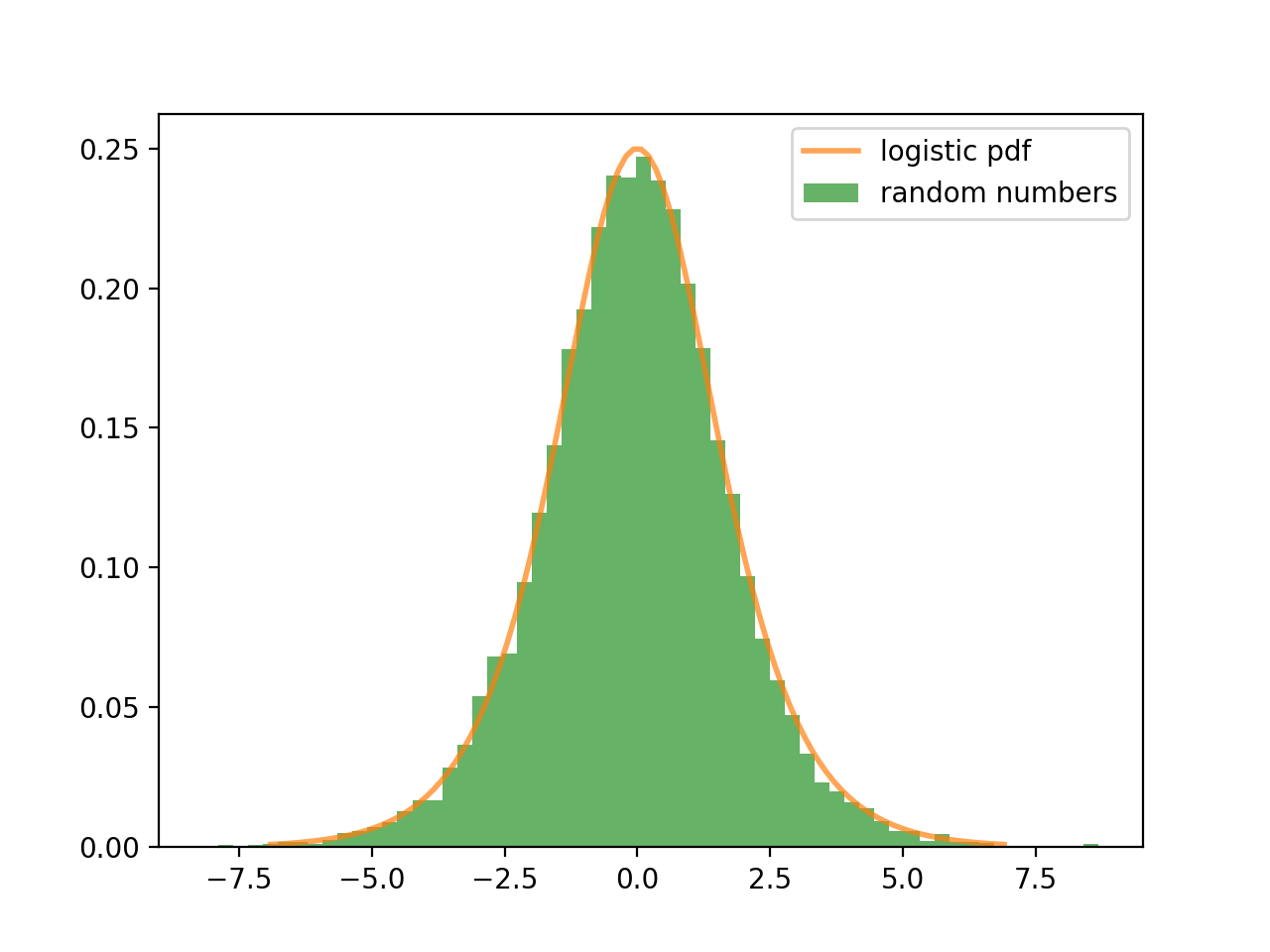
random_numbers_from_logistic = [inv_logistic_cdf(random_number)
                                for random_number in random_numbers]

로지스틱 확률 밀도 함수(pdf)와 위의 코드에서 생성한 난수의 히스토그램을 비교하면 아래와 같다. 생성한 난수는 로지스틱 확률 분포에서 추출한 난수가 맞다는 것을 알 수 있다.

logistic pdf

레일리 분포를 따르는 난수 생성기

이번에는 레일리 분포(Rayleigh Dist.)를 따르는 난수 생성기를 만들고 싶다. 역시나 레일리 난수 생성기는 없고, 기본 난수 생성기만 있다. 레일리 CDF는 다음과 같다.

\[F(x) = 1 - e^{-x^{2}/2}\]

기본 난수 생성기 $U$를 $F^{-1}$에 대입하면 레일리 분포를 따르는 확률 변수를 만들 수 있다.

\[F^{-1}(U) = \sqrt{-2log(1 - U)} \sim \text{Rayleigh}\]

이를 코드로 구현하면 아래와 같다.

# python3
import math
import random

def inv_rayleigh_cdf(u):
    return math.sqrt(-2 * math.log(1 - u))

# random samples from Unif(0, 1)
random_numbers = [random.random() for _ in range(10000)]

# random samples of Rayleigh Dist. through the inverse transform
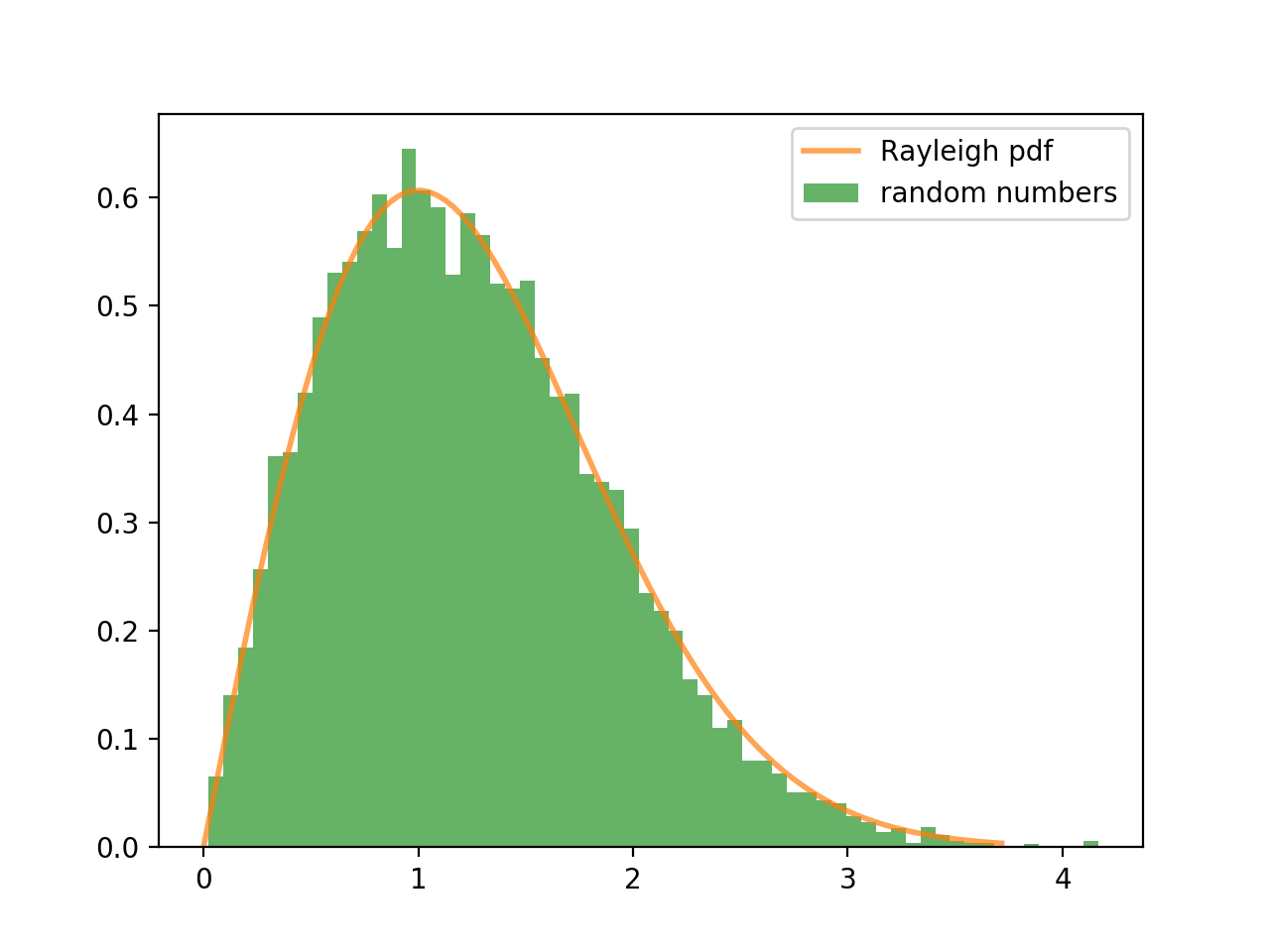
random_numbers_from_rayleigh = [inv_rayleigh_cdf(random_number)
                                for random_number in random_numbers]

역시나 생성한 난수로 히스토그램을 그려보면, 원하는 확률 분포에서 나온 것을 알 수 있다.

logistic pdf

절단된 정규 분포를 따르는 난수 생성기

정규 분포 난수 생성기는 거의 모든 프로그래밍 언어가 제공한다. 그러나 특정 구간에서만 추출한 정규 분포 난수가 필요하다면 일반적인 정규 분포 난수 생성기를 사용할 수 없다. 이런 경우에는 역함수에 대입할 기본 난수의 범위를 적절하게 조정하여 절단된 정규 분포 난수 생성기를 만들 수 있다.

난수를 추출하고 싶은 절단된 정규 분포는 아래와 같다.

\[X \sim N(\mu, \sigma^{2}) \, \text{I}(a < X < b)\]

평균이 $\mu$, 표준 편차가 $\sigma$인 정규 분포를 따르는 난수를 추출하고 싶지만, 그 난수의 범위는 (a, b)에 속해야만 하는 상황이다. 추출 난수의 범위가 $a < X < b$ 이므로, 기본 난수의 범위를 이에 맞게 조정해야 한다.

\[\begin{align} u_{a} & = \Phi((a - \mu) / \sigma) \\ u_{b} & = \Phi((b - \mu) / \sigma) \end{align}\] \[(\Phi \text{ is CDF of }N(0, 1))\]

이제 기본 난수 생성기의 범위를 $u_{a} < U < u_{b}$로 제한한다.

\[\begin{align} U & \sim Unif(u_{a}, u_{b}) \\ X & = \sigma \, \Phi^{-1}(U) + \mu \sim N(\mu, \sigma^{2}) \, \text{I}(a < X < b) \end{align}\]

이 과정에서 원하는 분포의 절단된 범위를 기본 난수의 절단 범위로 넘기는 부분이 중요하다. 즉, $a < X < b$ 의 범위를 $u_{a} < U < u_{b}$ 로 변환시키는 과정이 추가되었다. 이제 절단된 기본 난수를 역함수에 대입하여 절단된 정규 분포 난수를 생성할 수 있다.

확률 분포 $N(2, 9)\,\text{I}(1<X<5)$ 를 따르는 난수 생성기를 만들면 아래 코드와 같다.

# python3
from random import uniform
from scipy.stats import norm

def trucated_norm_rng(size, mu=0, sigma=1, lower_bound=None, upper_bound=None):
    u_lower = norm.cdf(lower_bound, mu, sigma) if lower_bound is not None else 0
    u_upper = norm.cdf(upper_bound, mu, sigma) if upper_bound is not None else 1
    rns_unif = (uniform(u_lower, u_upper) for _ in range(size))
    return (norm.ppf(rn_unif, mu, sigma) for rn_unif in rns_unif)

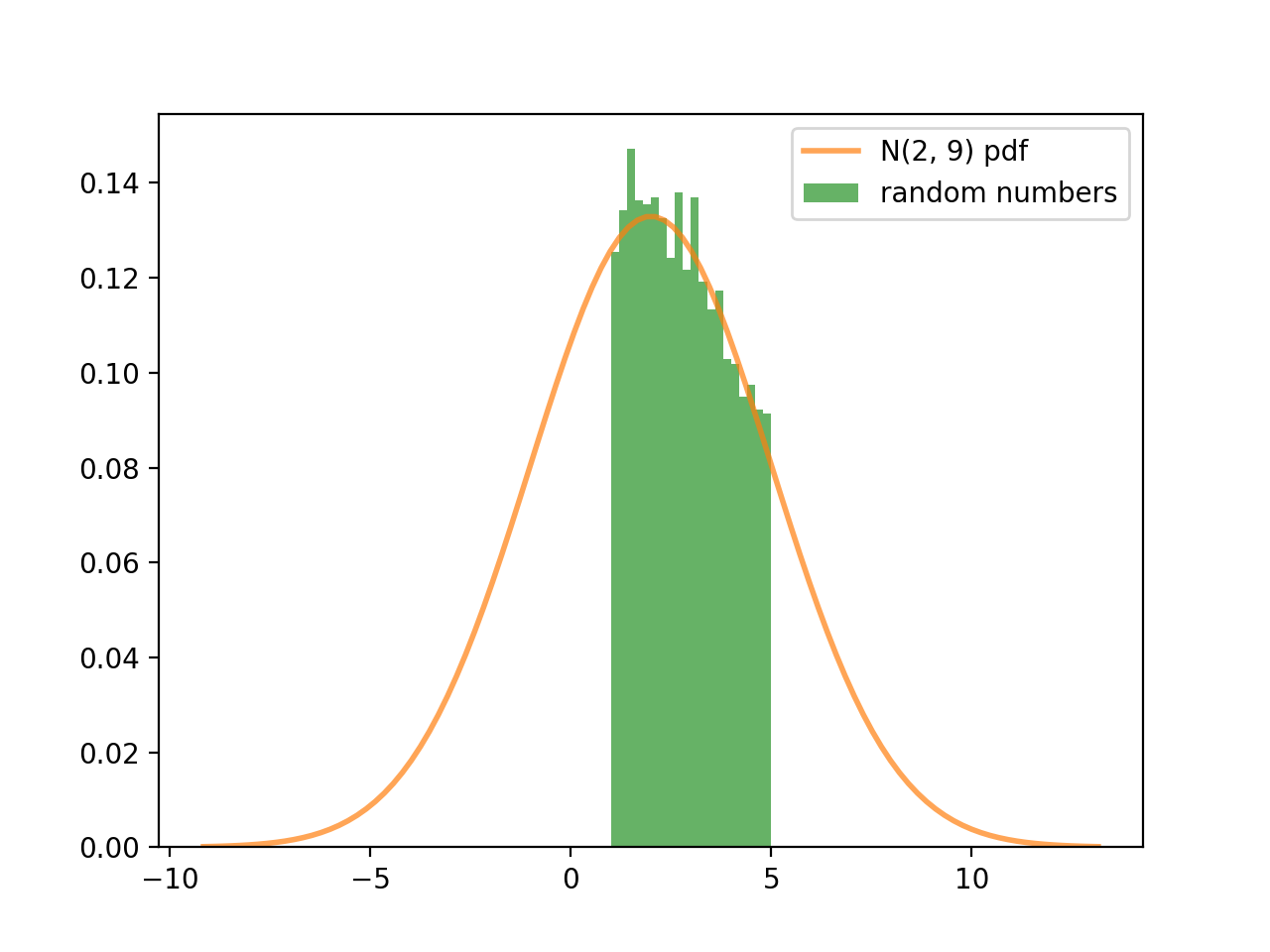
rng = trucated_norm_rng(10000, mu=2, sigma=3, lower_bound=1, upper_bound=5)

위의 코드에서 생성한 난수의 히스토그램을 보면 원하는 정규 분포의 원하는 범위 내에서만 추출된 것을 알 수 있다.

truncated normal pdf

결론

물론 대부분의 프로그래밍 언어는 로지스틱 난수 생성기 등을 제공한다. 따라서 위와 같은 번거로운 과정을 거치지 않고도 원하는 시뮬레이션이 가능하다. 문제는 그렇지 않은 경우인데, 혹시라도 누가 만들어놓은 모듈이 있는지 찾아 헤매다가, 불안함을 안고 검증되지 않은 함수를 사용하는 것보다는 직접 만드는 것이 속 편하다. 예외적인 경우지만, 기존 확률 분포를 변형시켜서 사용해야 할 때는 만들어 쓸 수 밖에 없다. 위의 방법은 누적 분포 함수의 일반적인 성격만 만족하면 기존에 정의되어 있지 않은 확률 분포에 대해서도 적용할 수 있기 때문에 유용하다. 원하는 어떤 형태의 분포에서든 난수를 만들어 낼 수 있다.

실무에서 이와 비슷한 문제가 있었는데, 당시에는 R 프로세스를 따로 실행하여 계산하는 방식으로 해결하였다. 물론 R에서도 지원하지 않는 확률 분포라면 만들어 써야 한다. 다시 같은 상황과 마주친다면 다른 프로세스를 따로 실행시키지 않고, 프로젝트 언어를 이용해 난수 생성기를 만들어 쓸 것이다.

통계와 개발을 함께 공부하는 건 재미있는 경험이다. 통계를 먼저 공부했지만, 개발을 하면서 예전에 알던 것을 재발견하는 경우가 많다. 반대로 개발을 잘 하기 위해서 통계 공부를 더 열심히 해야할 필요도 생긴다.

참고

누적 분포 함수의 역함수를 수식으로 정리할 수 없는 경우가 있다. 이 경우에는 역함수의 근사값을 구하는 과정이 필요하다.
$F(X)$의 의미를 이해하는 것이 중요하다. $F(x)$는 확률 분포마다 제각각 다른 함수다. 그러나 확률 변수의 누적 분포 함수에 확률 변수 자신을 대입하면 또 다른 확률 변수, $F(X)$가 된다. 그리고 이렇게 새로 만들어진 확률 변수는 항상 균등분포를 따른다. $F(X) \sim Unif(0, 1)$. $F(x)$가 어떤 함수든 상관없이 이 관계가 성립한다.
$F^{-1}$는 보통 inverse CDF라고 하지만, quantile function 혹은 percent point fuction(ppf)라고도 부른다. scipy.stats에는 확률 분포마다 ppf를 따로 구현해놓았다.
이 글은 아래 참고 자료를 이용하여 작성하였다.

-[|]- Box and Whisker

특정 확률 분포를 따르는 난수 생성기 만들기