문제 상황

푸시 메시지 타이밍 찾기에서 언제 유저에게 메시지를 보내는 것이 좋을지 설명하였다. 이전에는 유저의 접속 시간 분포를 경험적으로 도출해서 확률을 계산하였다. 여기서는 아래와 같은 질문에 대답하고자 한다.

• 만약 오전 11시까지 유저가 접속하지 않았다면, 오늘 내로 유저가 접속할 확률은 얼마일까?

푸시 메시지 타이밍 찾기에서도 위와 비슷한 문제에 대해 설명을 하였다. 하지만 문제가 달랐는데, 이전 글에서는 유저가 접속했다는 가정하에서 어떤 시간대에 접속할 확률이 높은지를 살펴보았기 때문이다. 지금은 조건부 확률을 활용해서 위의 질문에 대답한다. 데이터 측면에서는 단순한 세션 막대기를 사용하는 것이 아니라 날짜 구분이 있는 세션 막대기를 사용한다. 즉, 특정 날짜의 언제 접속을 했는지 안했는지에 대한 정보를 활용한다.

날짜가 기록된 세션 막대기

로그인 시각과 로그아웃 시각으로 가로 길이가 결정된 세션 막대기를 날짜라는 세트로 묶는다. 이 세트는 세션 막대기를 담는 일종의 케이스라고 볼 수 있다. 편의상 시간 단위로만 막대기를 구성한다. 하루 단위의 세션 막대기 포장 상자는 아래와 같은 모양이다. 24시간에 해당하는 칸으로 구성되어 있고, 접속한 시각에는 칸을 채운다.

예를 들어, 어떤 유저 한 명의 세션 기록이 다음과 같다면, 세션 막대기를 아래 그림처럼 나타낼 수 있다.

cid, datetime, event
a32e1bfb-62aa-4b04-8453-0b8b67cd4ca3, 2015-03-01 10:00:00, login
a32e1bfb-62aa-4b04-8453-0b8b67cd4ca3, 2015-03-01 14:00:00, logout
a32e1bfb-62aa-4b04-8453-0b8b67cd4ca3, 2015-03-01 19:00:00, login
a32e1bfb-62aa-4b04-8453-0b8b67cd4ca3, 2015-03-01 21:00:00, logout
a32e1bfb-62aa-4b04-8453-0b8b67cd4ca3, 2015-03-02 01:00:00, login
a32e1bfb-62aa-4b04-8453-0b8b67cd4ca3, 2015-03-02 03:00:00, logout

유의할 점은, 위의 그림이 특정 유저 한 명의 단 하루에 대한 기록이라는 점이다. 다음 날이 되면 새로운 세션 상자에 세션 정보를 기록한다.

10일 동안 같은 유저의 접속 기록을 세션 상자로 나타내면 아래와 같이 10개의 상자가 나타난다. 이제 확률을 계산할 수 있다. 실제 계산을 하기 전에 ‘조건부 확률’에 대해서 간략하게 설명한다.

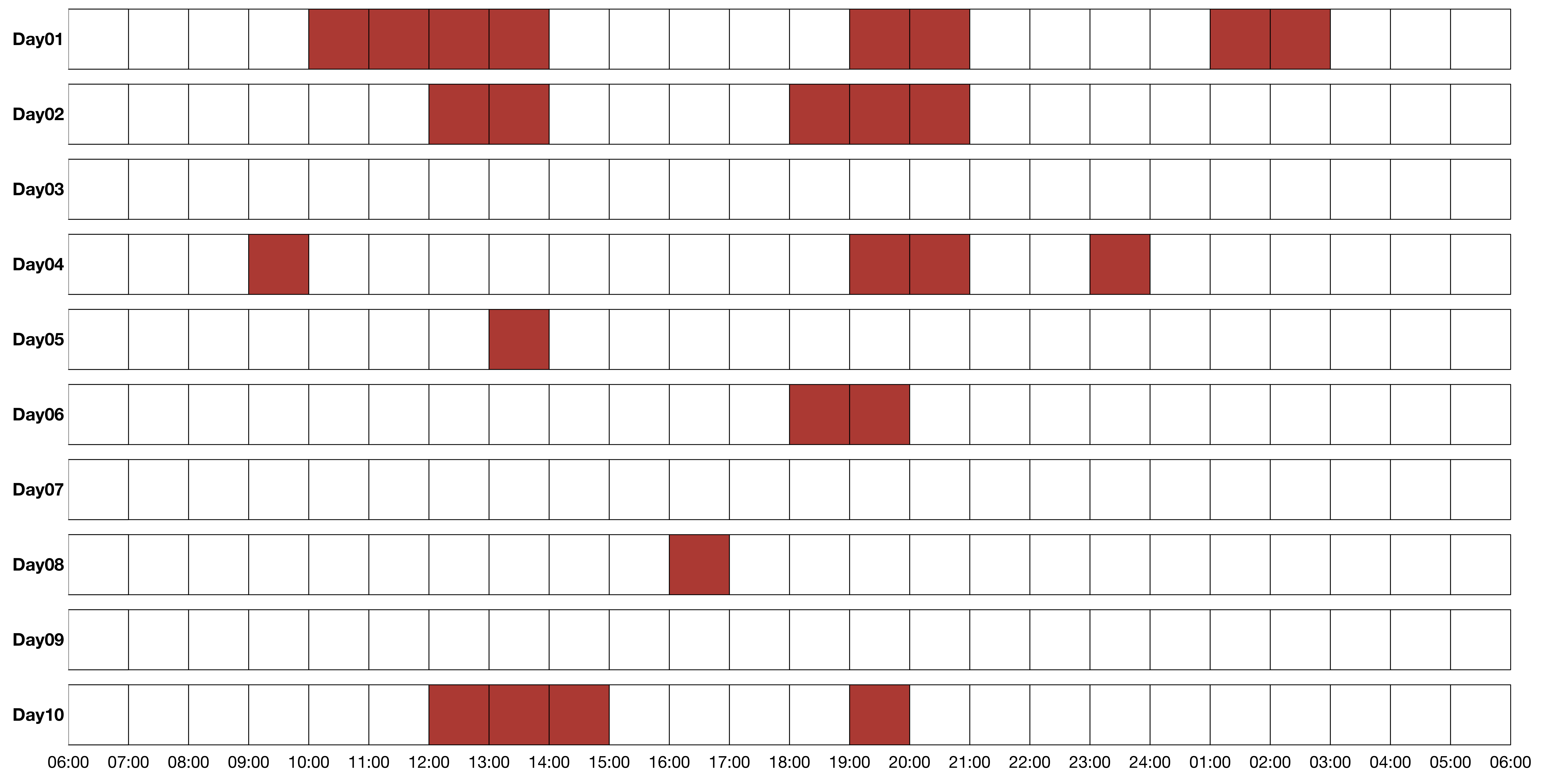
그런데 왜 하루의 시작과 끝이 오전 6시일까? 하루의 구분은 매우 개인적이다. 서비스를 사용하던 유저가 밤 12시를 지나는 순간부터 갑자기 새로운 날의 새로운 경험을 하지는 않는다. 단지 오후 11시 59분에도 사용하던 서비스를 자정이 넘어서도 이어서 사용할 뿐이다. 자정을 기준으로 데이터를 다루면 하나였던 세션 막대를 인위적으로 2개로 만든다. 이는 유저 입장에서 분석을 하는 것이 아니다.

반드시 오전 6시를 기준으로 잡아야하는 것은 아니다. 기술적으로 설명하면, 세션 막대기의 인위적인 단절이 가장 적게 일어나는 시각이 가장 좋은 하루의 기준이다. 실제로 몇 시가 적당한지는 서비스마다 다르다. 역시나 기준은 사람이 똑똑하게 정하고, 계산은 기계에게 맡긴다.

조건부 확률의 이해

조건부 확률(conditional probability)이란 특정 사건이 일어났다는 조건이 주어진 상태에서, 다른 사건이 일어날 확률을 의미한다. 예시로 이해하자. 다음과 같은 두 가지 사건이 있다.

• $L$: 그녀가 나를 사랑(Love)하는 사건
• $S$: 그녀가 나를 보고 웃는(Smile) 사건

$P(L)$은 그녀가 나를 사랑할 확률이다. 확률을 ‘불확실한 사건이 일어날 것이라는 믿음의 정도’라고 이해한다면, $P(L)$은 그녀가 나를 사랑한다는 믿음의 크기다. 그런데 재미있는 사건이 일어난다. 요즘 그녀가 나를 보면 자주 웃는다. $P(S)$는 그녀가 나를 보면 웃는 확률이다. 확률을 ‘불확실한 사건이 일어나는 비율’이라고 이해한다면, $P(S)$는 그녀가 나를 보면 웃는 비율이다.

그녀가 나를 보고 자주 웃기 전에 그녀가 나를 사랑하리라는 믿음은 아주 약했다. 즉, $P(L)$은 아주 작은 숫자였다.

하지만, 그녀가 나를 보며 자주 웃는 것을 보니 이 믿음이 커졌다. 이를 확률로는 조건부 확률, $P(L|S)$로 표현한다. $S$라는 사건이 일어났다는 조건 하에서, $L$이라는 사건이 일어날 확률이다. 아래는 그녀가 나를 보며 웃을 경우에, 나를 사랑할 가능성이 얼마인지 나타내는 숫자다.

과도하게 믿음이 올라갔는지 모르겠다. 어쩌면 나를 보고 절대로 웃지 않는 그녀가 나를 더 사랑할지도 모른다. 그러나 여기서 중요한 것은 ‘그녀가 나를 보고 웃는다’는 새로운 정보를 확률에 반영했다는 점이다. 이 정보가 있기 전에는 단순한 짐작이었지만, 새로운 정보가 추가되었으니 이 짐작을 수정해야 한다. 여기서는 주어진 정보를 최대한 활용한다는 점이 중요하다.

물론 새로운 정보가 항상 의미 있는 것은 아니다. 아래와 같은 새로운 사건을 추가하자.

• $O$: 꽃잎이 홀수(Odd)인 사건

‘그녀가 나를 사랑한다, 사랑하지 않는다, 사랑한다, 사랑하지 않는다….’ 꽃잎을 하나씩 따면서 그녀의 사랑을 점쳐 본다. 그러나 꽃잎의 숫자가 홀수이든 짝수이든 그녀가 나를 사랑하리라는 믿음은 변하지 않는 것이 합리적이다.

ref.: John K. Kruschke (2010), Doing Bayesian Data Analysis: A Tutorial with R and BUGS, Academic Press - See ch4.

조건부 확률을 이용해서 유저가 접속할 확률 계산하기

글의 시작 부분에서 제기한 문제를 다시 보면 아래와 같다.

• 만약 오전 11시까지 유저가 접속하지 않았다면, 오늘 내로 유저가 접속할 확률은 얼마일까?

이를 조건부 확률로 바꾸기 위해서 적절한 사건을 먼저 정의한다.

• $B_{t}$: 유저가 하루 중, $t$시점 전(Before)에 접속하는 사건
• $A_{t}$: 유저가 하루 중, $t$시점 후(After)에 접속하는 사건
• $X^{c}$: $X$라는 사건이 일어나지 않는 사건, X의 여사건(complementary event)

우리의 질문을 조건부 확률로 표현하면 아래와 같다.

이는 $t$시점 이전에 유저가 접속하지 않았다($B_t^c$)는 조건 하에서, $t$시점 이후에 유저가 접속($A_t$)할 확률이다. 조건부 확률을 실제 계산하는 과정은 아래와 같다.

분모는 $t$시점 이전에 유저가 접속하지 않은 사례($B_t^c$)를 모두 센다. 단순히 해당 사건이 얼마나 있었는지 빈도를 구하는 과정이다. 분자는 $t$시점 이전에 유저가 접속하지 않았지만 이후에 접속한 사례($A_t \cap B_t^c$)를 모두 센다. 이 역시 두 사건이 동시에 일어나는 빈도를 계산하는 과정이다.

날짜가 기록된 세션 막대기를 통해서 위의 수식의 분모를 계산한다. $t$시점 이전에 유저가 접속하지 않는 사건($B_t^c$)의 빈도를 세면 아래와 같이 8번이다.

수식의 분자를 계산하면 아래와 같다. $t$시점 이전에 유저가 접속하지 않았지만 이후에 접속한 사건($A_t \cap B_t^c$)의 빈도를 세면 아래와 같이 5번이다.

이를 통해 조건부 확률을 구하면 아래와 같다. 만약 오전 11시까지 유저가 접속하지 않았다면, 오늘 내로 유저가 접속할 확률은 $0.625$다. 반대로, 오전 11시까지 유저가 접속하지 않았을 때, 오늘 내로 유저가 접속하지 않을 확률은 $1 - 0.625 = 0.375$다.

푸시 메시지 타이밍 찾기에서는 시간이 흐름에 따라 시점이 변하면서 유저의 접속 확률도 변화하는 과정을 설명하였다. 조건부 확률을 이용한 위의 사례에서도 시점 $t$를 변화시키며 확률을 계산할 수 있다. 이 과정은 비교적 간단하므로 자세한 설명은 푸시 메시지 타이밍 찾기로 대체한다.

만약 조건부 확률을 사용하지 않으면 확률 값은 어떻게 달라질까? 조건부 확률을 사용하지 않으면 우리의 질문은 다음과 같이 단순해 진다.

• 오전 11시 이후에 유저가 접속할 확률은 얼마일까?

오전 11시 이후에 유저가 접속한 모든 경우를 세면 7번이다. 따라서 아래와 같이 $0.7$의 확률 값을 얻을 수 있다.

조건부 확률로 계산했을 때, 오전 11시 이후에 유저가 접속할 확률이 낮아진 것을 알 수 있다.

조건부 확률을 적용했을 때, 확률 값이 변한 것은 매우 중요한 의미를 갖는다. $t$시점에서의 새로운 정보(‘유저는 $t$시점전에 접속하지 않았다’)를 활용할 때와 그렇지 않았을 때의 의사결정은 달라질 수 있기 때문이다.

‘접속 시간 분포’와의 차이

푸시 메시지 타이밍 찾기에서는 접속 시간 분포를 구했는데, 날짜가 기록된 세션 막대기로도 만들 수 있다. 전과 같이 세션 막대기를 시간 축에 차곡차곡 쌓아 더미를 만든다.

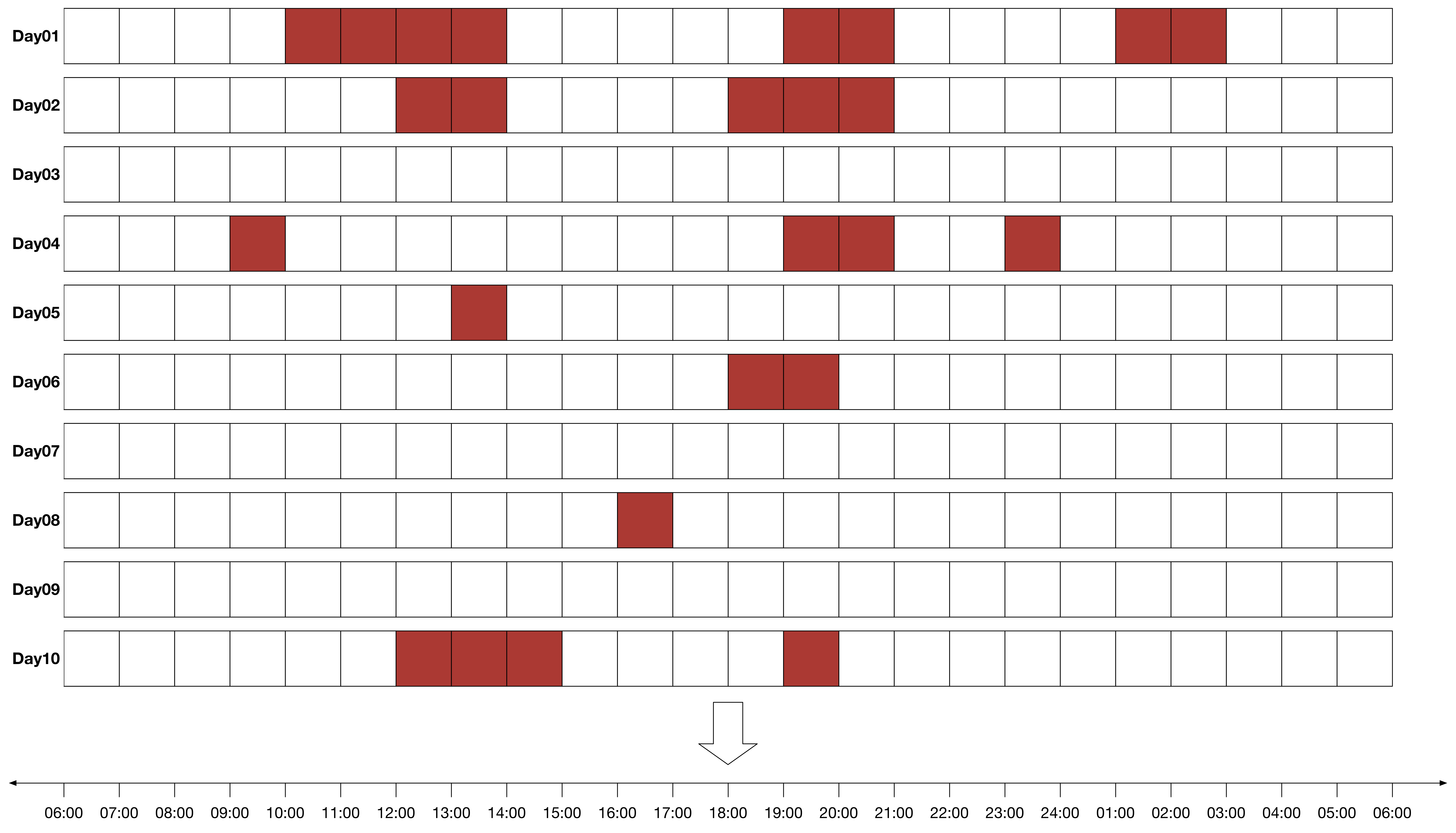
세션 찰흙 막대기를 아래와 같이 쌓아서 유저의 접속 시간 분포를 만들 수 있다. 이 과정에서 알 수 있는 것은 ‘접속 시간 분포’를 만들면서 유저가 접속하지 않은 3일(Day03, Day07, Day09)의 정보가 사라졌다는 점이다. 즉, 세션 막대기에서 날짜(Day00)를 지웠기 때문에 10일 중 접속하지 않은 날이 3일이라는 정보는 알 수 없게 되었다. 따라서 ‘접속 시간 분포’는 유저가 접속한 날 중에서 접속한 시간이 언제인지 알려주는 정보다.

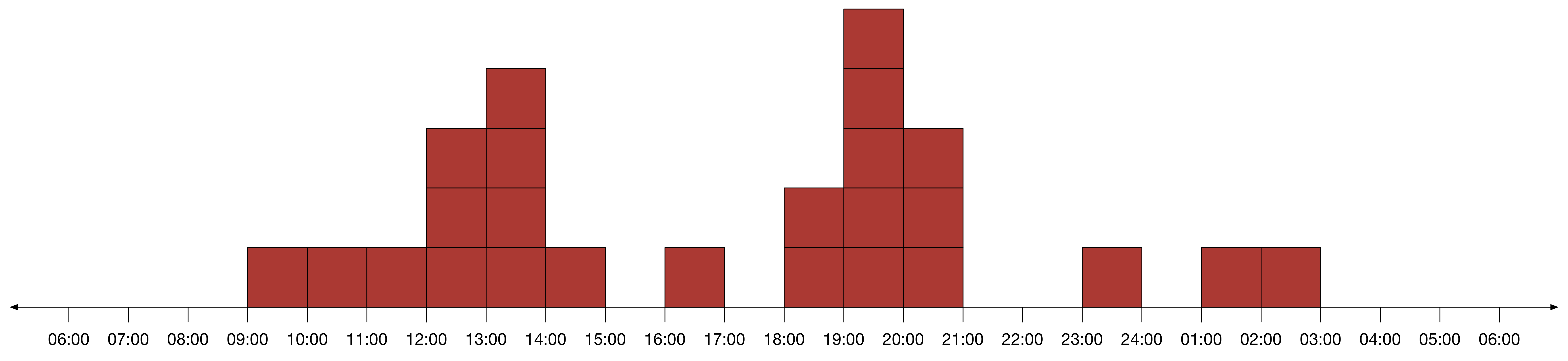
이를 토대로 유저가 오전 11시 이후에 접속해 있을 확률은 아래와 같다.

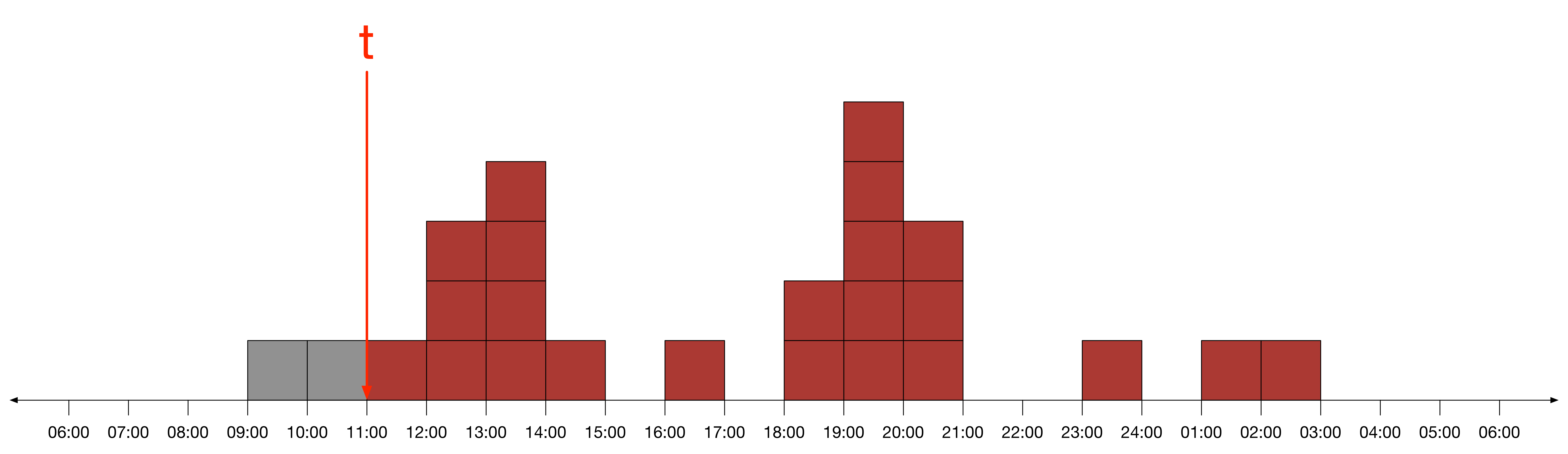
이는 유저가 오늘 접속한다는 가정 하에서, 오전 11시 이후에 접속해 있을 비율이 어느 정도인지 나타낸다. 쉽게 말해서 유저는 과거에 총 25시간 동안 서비스를 이용하였고, 그 중 23시간을 오전 11시 이후에 사용하였다. 따라서 앞으로 이 유저가 서비스를 이용할 시간대도 이와 유사할 것이라고 믿는 것이 타당하다.

실행상의 어려움

이탈 유저 탐색

이탈 유저에 대한 구분이 필요하다. 만약 어떤 유저가 100일 전에 서비스를 처음 이용하고, 최근 90일 동안 서비스를 사용하지 않았다고 가정하자. 이 유저의 접속 세션 기록을 그대로 사용하면, 접속 확률을 계산하는 것이 무의미하다. 따라서 이미 이탈한 유저에 대해서는 접속 확률을 구해서 관리할 대상으로 삼지 않는 것이 합리적이다.

시스템

‘유저가 언제 자주 접속하는가’라는 문제를 넘어서, 조건부 확률을 구하기 위해서는 이전 글에서 언급한 것보다 더 많은 데이터가 필요하다. 세션 막대에 대한 날짜를 함께 기록하여 관리하고, 매 시점이 변경될 때마다 조회하고 확률을 계산해야 한다. 만약 시간 단위가 아니라 더 세밀한 대응을 원한다면 문제는 더 복잡해진다. 자동화 시스템을 아주 잘 만드는 수 밖에 없다. 유능한 개발자의 도움을 꼭 받도록 한다. 필요하다면 유저에 대한 액션과 전략의 범위를 한정하고, 이에 대응할 수 있는 데이터만 기록한다.

활용안

최근 정보를 고려한 유저 관리

반드시 푸시 메시지가 아니더라도, 현 시점의 유저 접속 정보를 활용해서 유저에 대한 액션을 결정하는 과정에 활용할 수 있다. 착안은 푸시 메시지 최적화였으나, 맥락이 유사한 여러 사례에 활용할 수 있다. 유저가 접속할 확률을 이용해서 최적화가 가능한 액션을 상상해 보는 것이 좋겠다. 특히 타임 윈도우를 하루 단위가 아니라 그 이상으로 확장하면, 적당한 유저 이탈 관리 모형으로 활용 가능하다. 예를 들어, 하루를 일주일이나 그 이상의 시간 범위로 확장하면 특점 시점까지 접속하지 않는 유저에 대한 관리가 가능하다. 시간 범위가 커지면 고려할 사항도 많아지지만, 충분히 활용할 가치가 있다.