고객의 접속 세션 데이터를 이용해서, 유저의 이탈 가능성을 평가하는 방법을 정리한다.

기본 개념

‘이탈 기준 정하기’에서 데이터를 이용해 적절한 이탈 기준을 살펴보았다. 그리고 ‘개별 사용자를 고려한 이탈 측정하기’에서 유저 개인의 접속 특성을 고려한 이탈 척도를 살펴보았다. 종합하면, 유저가 특정 기간 동안 접속하지 않으면 이탈 유저로 정의하며, 유저 간의 비교를 위해서 이탈 위험 비율이라는 척도를 사용한다.

이 두 가지 개념을 이용하여, 모든 개별 유저에게 이탈 유무를 기록하고, 이탈 위험 비율을 계산하여 이탈 유무를 설명하는 통계적 모형을 만들어 본다. 간략하게 요약하면 아래와 같은 함수 \(f\)를 생각할 수 있다.

\[Probability(Churn_{k}=1) = f(RiskRatio_{k}=x)\]

Churn: 이탈 유무, 0 or 1
Risk Ratio: 이탈 위험 비율

즉, 유저의 이탈 위험 비율을 토대로 \(k\)라는 유저가 이탈할 가능성을 평가한다. 예를 들어, A라는 유저의 이탈 위험 비율이 2.2이라면, 위의 모형을 통해서 해당 유저의 이탈 가능성은 0.72라는 값을 얻을 수 있다.

\[Probability(Churn_{A}=1) = f(RiskRatio_{A}=2.2) = 0.72\]

이를 풀어서 설명하면, 자신의 평균 접속 주기보다 2.2배의 기간동안 접속이 없었던 유저 A는 이탈할 가능성이 72%라는 의미다. 이는 임의의 예시이며, 실제 데이터를 통해서 해당 모형을 간단하게 만들 수 있다.

데이터 소개

설명을 위해서 가짜 데이터를 사용한다. 가짜 데이터는 ‘fake log generator’를 사용하여 생성하였다. 모형을 단순화하기 위해서 유저의 세션 접속 기록은 일 단위로 변환한다. 즉, 하루에 아무리 자주 접속하더라도 해당 유저의 접속 기록은 1일 1회로 표시한다. 만약 시간 단위로 세션 기록을 확장한다면, 더 자세한 분석이 가능하나, 모형이 복잡해지므로 이 글에서는 일 단위로만 설명을 한정한다.

생성한 가짜 데이터는 아래와 같다. cid는 유저 아이디를 나타내며, datetime은 로그인 시간이다. 로그인 이벤트만 존재한다고 가정하므로, 이벤트 타입을 명시하는 컬럼은 만들지 않는다.

cid, datetime
a32e1bfb-62aa-4b04-8453-0b8b67cd4ca3,2015-01-01 00:07:06.503562
a32e1bfb-62aa-4b04-8453-0b8b67cd4ca3,2015-01-02 08:13:29.638174
a32e1bfb-62aa-4b04-8453-0b8b67cd4ca3,2015-01-05 18:23:40.235538
a32e1bfb-62aa-4b04-8453-0b8b67cd4ca3,2015-01-14 06:11:33.682871
a32e1bfb-62aa-4b04-8453-0b8b67cd4ca3,2015-01-16 01:15:42.775384
a32e1bfb-62aa-4b04-8453-0b8b67cd4ca3,2015-01-18 03:30:07.504791
...

가짜 데이터는 ‘fake log generator’의 make_multiple_cid_logs(3000, '2015-01-01', '2015-03-31', 2, .005) 함수를 사용하여 생성하였으며, 예제 파일 링크에서 다운로드 받을 수 있다. 새로 데이터를 생성할 경우, 예제 데이터와 다른 데이터가 생성된다.

데이터 가공

로그 데이터를 파일 형태로 확보했다면, 통계 모형을 만들기 전에 분석 가능한 형태로 변형해야 한다. 분석에 적합한 데이터 형태로 바꾸기 위해서 R의 dplyr 패키지를 사용한다. 데이터 분석에 적합한 데이터 형태에 대해서는 tidy data를 참고한다.

이탈 기준은 2015-03-31 시점에 마지막 접속 경과일이 8일을 초과하는 경우로 설정하였다. 이 기준은 ‘이탈 기준 정하기’의 내용을 참고하여 결정하는데, 해당 예제에서는 임의로 결정하였다. 경험적으로 이탈 기준은 7~14일 사이에서 결정되는 경우가 많은데, 서비스의 유저 행태에 따라 전혀 다르게 나타날 수 있다. 중요한 점은 이탈 기준의 길이에 따라 기민한 이탈 대응과 확실한 이탈 판단 사이에 상충 관계가 있다는 점이다.

데이터 정리 과정은 predict_churn.R을 이용하였다. 최종적으로 정리한 데이터는 아래와 같다.

                                    cid risk_ratio churn
0000c18d-988b-4055-bca2-3ba8cc08dd97  0.7105263     0
00093b5b-7945-491b-87d6-78b9e24283e6  0.3544304     0
0010e00f-7667-4194-8cd3-a4046618968c  0.2105263     0
001766d8-8418-4922-9b02-26609e68279b  0.7894737     0
0047b53b-156d-4a27-8170-5357375673a8  1.3521127     0
004b8db7-e799-4374-bf8d-25859cf2ddbd  0.2597403     0
0073ce9c-2d6a-480b-a219-4fb4f049a781  0.6800000     0
0083cb03-7059-41b8-b567-769f4b57cb68  1.8055556     1
00931bdf-085a-4d2c-8397-8b0647865c0c  2.8656716     1
00940491-2f54-4152-9779-7bdc125ec44f  0.7894737     0
..                                  ...        ...   ...

모형 만들기

모형의 기본 형태는 churn ~ risk_ratio와 같은 모습이다. 즉, 위험 비율로 이탈 여부를 설명하는 모형을 만든다. 설명하고자 하는 변수 churn이 이항 사건이기 때문에 여러가지 분석 방법 중에서 로지스틱 회귀 분석을 사용한다. 로지스틱 회귀 분석을 사용한 이탈 예측은 여러 분야에서 매우 많은 사례를 찾아볼 수 있다. R에서는 아래와 같이 glm 함수에 family=binomial() 을 지정하여 로지스틱 회귀 모형을 만들 수 있다. 마찬가지로 predict_churn.R을 이용하여 모형을 만든다.

fit <- glm(churn ~ risk_ratio, data = rr_logs, family = binomial())

그런데, 해당 모형은 일종의 순환 논리 오류를 가지고 있다. churn과 risk_ratio는 ‘마지막 접속 경과일’에 일정 부분 종속되므로, 상당한 정보를 공유한다. 따라서 해당 모형은 표면적으로 상당히 정확한 모형으로 보일 수 밖에 없다. 바꿔 말하면, 애초에 비슷한 변수 2개를 모형의 종속 변수와 설명 변수로 설정하기 때문에 모형 자체가 갖는 의미는 크지 않다. 그럼에도 불구하고 해당 모형이 유용한 것은 위험 비율이라는 공통된 척도로 유저의 이탈 가능성을 점진적으로 도출할 수 있다는 점이다.

만약, 모든 유저에게 이탈 기준을 7일로 설정하면, 마지막 접속일로부터 7일이 지나기 전에는 이탈 위험이 0이였다가, 7일이 지나는 순간 이탈 위험이 1로 건너뛴다. 그러나 이탈 위험 비율로 이탈 가능성을 나타내면, 유저의 평균 접속 주기와 비교해서 마지막 접속 경과일이 늘어날 때마다 이탈 위험이 점진적으로 증가한다.

해당 모형으로 만든 이탈 곡선은 아래와 같다. 기본 개념에서 소개한

\[Probability(Churn_{A}=1) = f(RiskRatio_{A}=2.2) = 0.72\]

식에서, 함수 \(f\)는 아래 그래프의 좌하단 수식으로 나타낼 수 있다. 함수 \(f\)를 대입하여 아래의 수식처럼 유저 A의 이탈 가능성을 계산할 수 있다.

\[P(churn=1) = \frac{1}{1+exp(9.3552 - 4.6795 \times 2.2)} = 0.72\]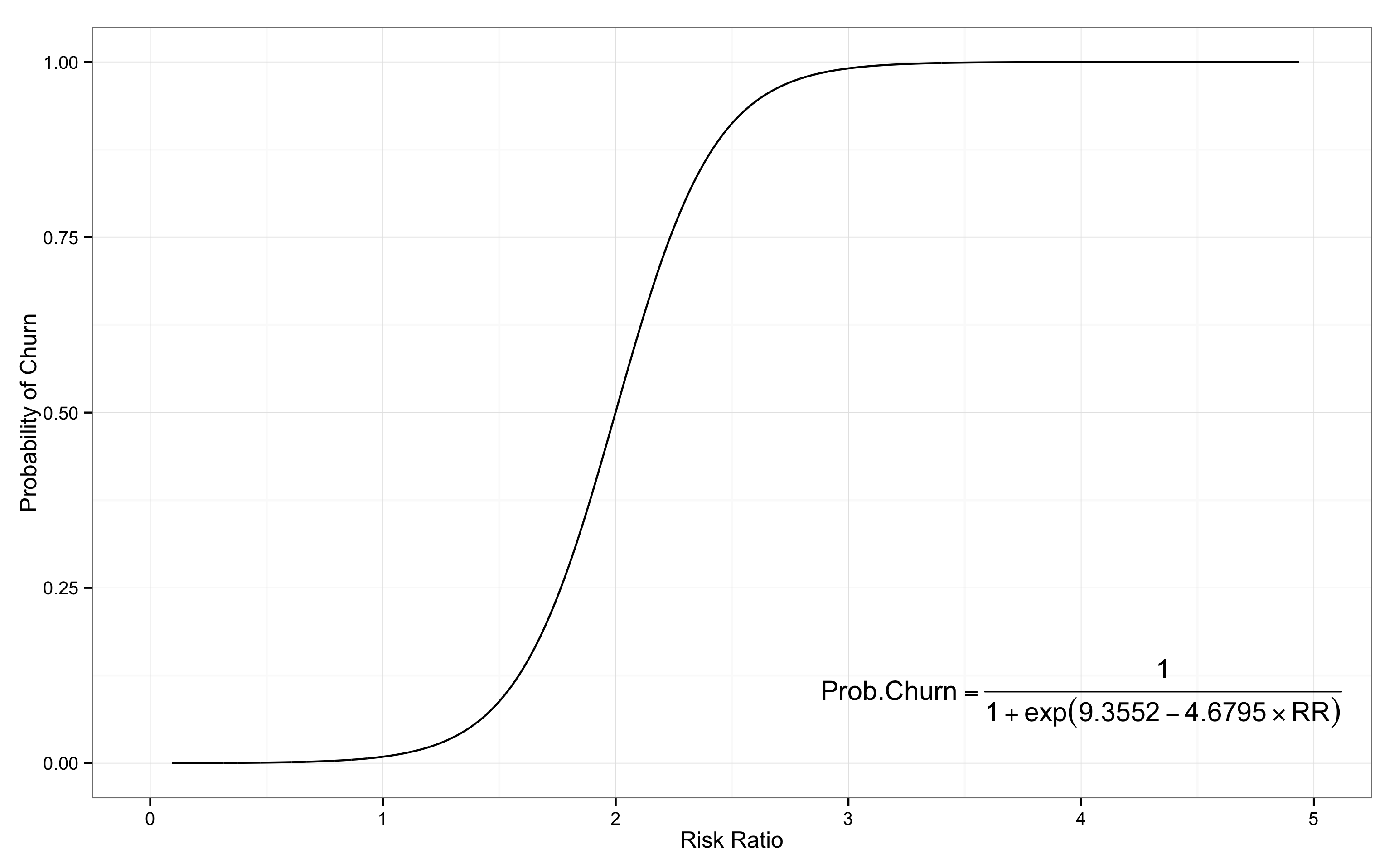

single_curve

위의 이탈 곡선을 살펴보면, 위험 비율이 1 이하일 때는 거의 이탈 가능성이 없다. 즉, 유저의 평균 접속 주기와 비슷하거나 그보다 더 짧은 기간 동안 접속이 없다면 유저의 이탈 가능성은 0이다. 그러나, 위험 비율이 2로 증가하면 유저의 이탈 가능성은 0.5로 나타난다. 이는 유저의 평균 접속 주기보다 2배 정도 긴 기간 동안 접속이 없다면 유저의 이탈 가능성은 50% 정도로 볼 수 있다는 의미다. 만약, 위험 비율이 3으로 증가하면 이탈 가능성은 거의 1이 된다. 다시 말해, 평균 접속 주기보다 3배나 긴 시간 동안 접속이 없었다면, 유저의 이탈 가능성은 100%가 된다.

위의 모형은 가짜 데이터를 사용하여 만들었으므로, 역시 가짜다. 다만, 충분히 일어날 수 있는 상황이며, 서비스의 종류나 유저의 행태에 따라 모형과 이탈 곡선은 판이하게 달라진다.

서로 다른 서비스의 비교

만약 두 개 이상의 서비스를 제공하는 경우라면, 개별 서비스마다 각각 이탈 곡선을 그릴 수 있다. 서로 다른 서비스는 서로 다른 이탈 곡선을 보인다. 유저의 접속 행태가 다르기 때문에 이탈 모형이 달라지기 때문이다. 만약 서비스 A와 서비스 B의 유저 접속 데이터를 이용하여 이탈 곡선을 도출한다면 아래와 같은 모습을 상상할 수 있다.

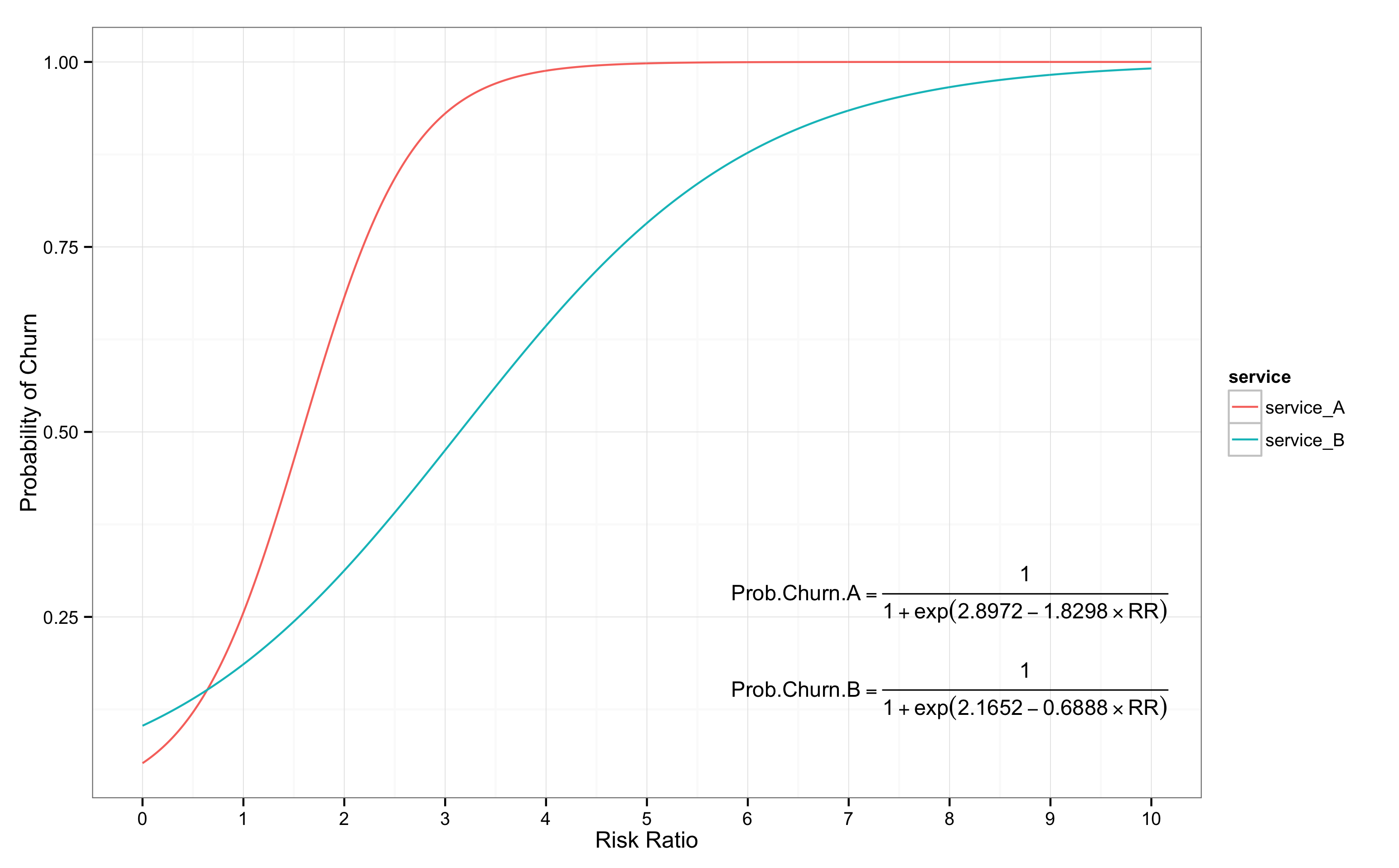
double_curve

A의 경우, 위험 비율의 증가에 따라 이탈 가능성이 상대적으로 가파르게 증가한다. 즉, 서비스 A의 경우에는 유저들이 약간만 오래 접속을 하지 않아도 이탈할 가능성이 높아진다. 그렇다고 서비스 A에 문제가 있다고 단언하기는 어렵다. 이는 서비스 자체 특성 때문일 수도 있으며, 유저들의 행동이 다르기 때문에도 나타날 수 있다. 다만, 매우 유사한 서비스라는 가정하에서는 이탈 곡선이 완벽한 S자를 그리면서 오른쪽으로 치우칠수록 긍정적이라고 볼 수 있다. 이는 평균 접속 주기보다 더 오랜 기간 접속하지 않더라도 재접속하는 유저가 많다는 의미이기 때문이다.

같은 서비스의 시계열 비교

이탈 곡선은 특정 시점을 기준으로 그린다. 위의 예시는 가상의 데이터에 대해서 2015-03-31 시점을 기준으로 이탈 모형을 도출하였다. 예제 데이터는 일 단위 접속 기록을 가정하였으므로, 하루에 하나의 이탈 곡선을 그릴 수 있다. 만약, 시간이 흐름에 따라 매일 이탈 곡선을 새롭게 도출한다면 이탈 곡선의 변동을 통해 유저의 행태 변화를 추적할 수 있다. 이를 나타내면 아래 그림과 같은 모습을 상상할 수 있다.

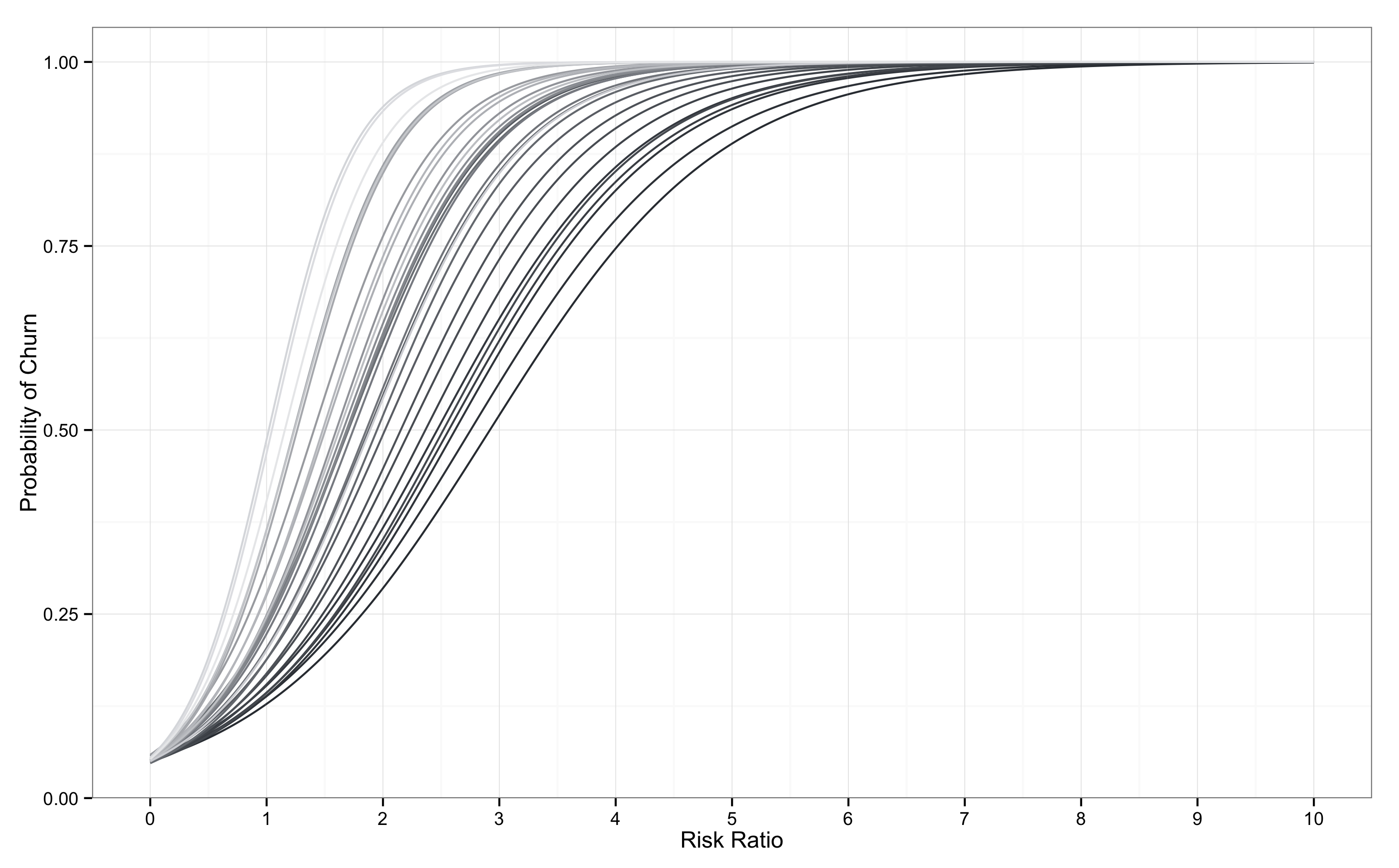
series_curve

위의 그림는 30일 동안 매일 하나씩, 총 30개의 이탈 곡선을 도출한 경우의 예시다. 밝은 색 곡선이 과거를 나타내며, 어두운 색 곡선이 가장 최근을 나타낸다. 위의 서비스는 시간이 지나면서 이탈 곡선이 오른쪽으로 이동하고 있다. 이는 동일 조건 하에서 매우 긍정적인 신호로 볼 수 있다. 유저가 평균 접속 주기보다 긴 시간 동안 접속하지 않아도 다시 서비스에 접속하는 경우가 점점 많아진다고 볼 수 있기 때문이다.

아래와 같이 반대의 경우도 생각할 수 있는데, 이탈 곡선이 좌측으로 이동하는 경우에는 유저들의 이탈이 가속화되고 있다고 추측할 수 있다. 극단적인 경우, y축의 절편이 0보다 훨씬 위로 이동하는 상황이 있는데, 기본적인 이탈률이 매우 높을 때 나타날 수 있는 모습이다. 즉, 아무리 유저가 접속 주기보다 짧은 시간동안 접속하지 않더라도 대부분의 유저가 이탈한다면 이탈 가능성은 항상 높게 나타날 수 밖에 없다.

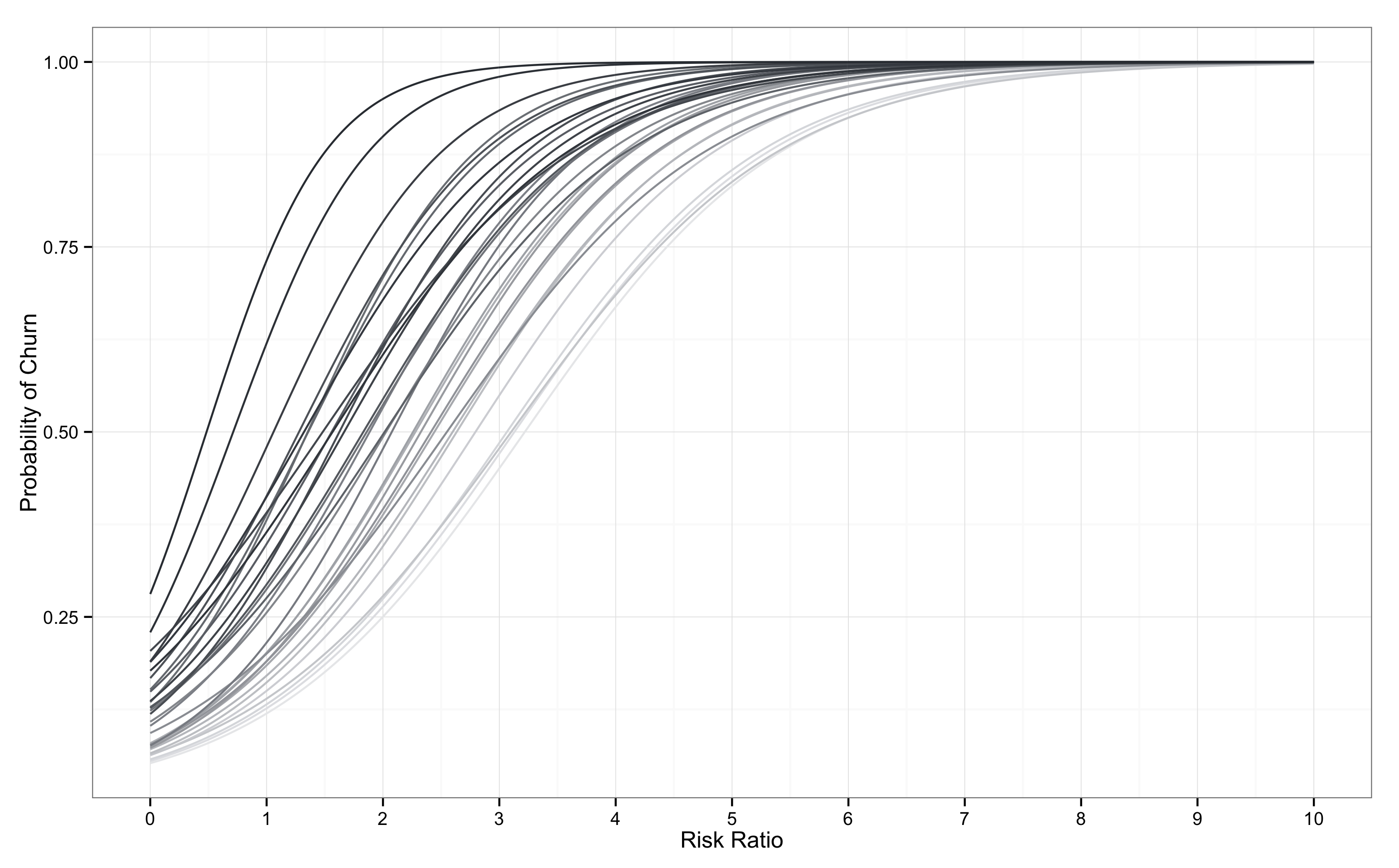
series_bad_curve

활용안

시간 경과에 따른 이탈 곡선의 변화

동일 조건 하에서, 이탈 곡선이 완벽한 S자에 가깝고 우측으로 치우칠수록 건강한 서비스라고 할 수 있다. 매일 변화하는 이탈 곡선의 변동을 추적하면 유저의 접속 패턴에 대한 평가가 가능하다. 서비스 시작부터 이탈 곡선을 나타낸다면, 서비스의 현 상황이 과거와 비교하여 어떻게 변했는지 알 수 있다.

서비스 간 이탈 곡선의 비교 및 분류

서비스 상호 간에 이탈 곡선을 비교하면 다른 변수를 통제한 상황에서 어떤 서비스가 더 건강한지 평가할 수 있다. 아울러 여러 서비스를 한꺼번에 비교하면 서로 비슷한 서비스와 다른 서비스를 구분할 수 있다. 여러가지 기준으로 이탈 곡선의 클러스터가 형성된다면, 서비스의 특성에 따른 이탈 곡선이 도출 가능하다. 각 클러스터의 대표 이탈 곡선을 만들고, 이와 다른 모습을 보이는 서비스는 더 많은 관심을 기울인다.

이탈 곡선에 따른 유저 분류

이탈 곡선을 사용하여 유저의 이탈 가능성에 따라 유저 구분이 가능하다. 이탈 가능성이 높은 유저를 따로 관리하고 싶다면, 이탈 곡선을 활용하여 해당 그룹만 추출하여 타켓 마케팅의 대상으로 삼을 수 있다. 또한, 이미 확실히 이탈한 유저에 대해서는 re-acquisition 전략을 수립하여 대응한다. 개별 유저의 이탈 가능성 추이를 추적하여 유저의 접속 패턴을 기민하게 관찰할 수 있다.

이탈 곡선과 유저 가치의 결합

유저의 기대 가치를 계량화 한다면, 이탈 곡선과 결합하여 이탈 가능성이 높으면서 가치가 큰 유저를 먼저 관리할 수 있다. 이는 고객의 LTV(life-time value)를 활용한 전형적인 고객 관리 방식이다. 유저의 기대 가치와 이탈 확률을 결합하면, 개별 유저에 대해서 기대 이탈 가치(expected churn value)를 계산할 수 있다. 가치가 높은 유저의 이탈 가능성이 높아진다면, 미래 수익을 잃게 되므로 해당 유저군의 이탈을 막는 것은 시급한 문제다.

한계점

앞서 이야기한 것과 같이, 종속 변수(‘이탈 유무’)와 설명 변수(‘이탈 위험률’)가 같은 변수(‘최종 접속 경과일’)에 공통적으로 연결된다. 태생적으로 상호 상관이 큰 변수들을 이용한 회귀 모형이므로 통계적 모형으로서의 가치는 거의 없다. 편의상 ‘이탈 예측’이라고 부르나, 실제로 예측(prediction)이라고 할 수 없다. 이는 ‘평균 접속 주기’와 ‘최종 접속 경과일’, ‘이탈 기준’이라는 3개 변수의 관계를 잘 나타내기 위해서 통계적 모형을 차용한 방법론에 불과하다. 따라서 예측 모형의 범주에서 사용하는 것은 피하고, 이탈 가능성을 나타내는 또 다른 척도로 활용하는 것이 적절하다.

이탈 곡선의 활용안에서 보았듯이, 서비스를 더 좋게 만들거나, 더 재미있게 만드는 작업에 도움을 주기 어렵다. 마케팅 관점에서 유저를 잘 관리하기 위한 도구로는 유용하나, 왜 유저가 이탈하는지, 무엇이 문제이므로 어디를 고쳐야 하는지에 대한 대답을 주지 못한다. 결국, 다른 성과 지표들과 유사한 문제점을 갖는데, 사후 약방문이 될 가능성이 높다. 이탈 곡선이 좌측으로 한참 밀리고, 기본 이탈 가능성이 0보다 많이 높아진 후에야 이를 인지하고 개선책을 마련하기 위해서 노력한다면, 이미 늦다. 되도록 서비스 초기부터 모니터링 대상으로 삼아서, 유저 접속 패턴의 변화를 빨리 알아차릴 수 있는 경고등으로 삼는 것이 유용하다.

-[|]- Box and Whisker

이탈 예측하기