확률형 아이템을 위한 다항 분포
이전 글: 온라인 게임에서의 이항 분포
온라인 게임의 확률형 아이템을 이항 분포와 다항 분포로 설명한다.
확률형 아이템
‘확률형 아이템’, ‘캡슐형 아이템’, ‘랜덤 박스’, ‘가챠폰(gachapon)’ 혹은 ‘가챠(gacha)’ 등으로 불리는 온라인 게임 내 유료 아이템이 있다. 이는 오프라인에서 판매하는 캡슐형 뽑기 완구를 온라인 게임 내에 이식한 형태다. 반투명한 캡슐에 장난감이 담겨 있어서, 실제 돈을 내고 뽑아서 열어보지 않으면 내용물을 알 수 없는 점이 꼭 닮아 있다. 기본적인 구조는 즉석 복권과도 유사하다. 몇 가지 상품이 나오게 되어 있고, 각 상품이 나올 확률은 내부적으로 정해져 있다. 보통 좋은 상품이 나올 확률은 매우 낮다.

많은 부분 유료화(free-to-play) 게임의 주요 매출 창구이기 때문에, 게임 개발사 입장에서 확률형 아이템은 매우 중요하다. 플레이어 입장에서는 돈을 내고 원하는 아이템을 얻고자 노력하기 때문에 얼마나 돈을 쓰고 아이템을 얻을 수 있는지 궁금하다. 확률형 아이템을 구매하고 그 결과를 확인하는 행위도 넓은 의미에서는 게임 플레이 경험이기 때문에 적절한 성공 확률을 결정하는 것은 재미있는 게임을 만드는 데 핵심적인 역할을 한다.
확률형 아이템 단순화 하기 - 이항 분포
확률형 아이템도 그 결과가 불확실하므로 일종의 시행(trial)이다. ‘확률’과 ‘시행’에 대해서는 이전 글인 ‘온라인 게임에서의 이항 분포’를 참고한다. 확률형 아이템은 그 결과가 2개가 아니므로 이항 분포(binomial distribution)로 설명할 수 없다. 그러나, 확률형 아이템에서 원하는 아이템이 단 한 가지라면 결과를 ‘성공’과 ‘실패’로 단순화시킬 수 있다. 원하는 아이템이 나오면 ‘성공’으로, 다른 아이템이 나오면 ‘실패’로 간주한다. 혹은 비교적 가치가 높은 아이템을 그룹으로 묶어서 해당 아이템 중에 하나가 나오면 ‘성공’, 그렇지 않으면 ‘실패’로 간주할 수 있다. 이렇게 사건을 단순화시키면 확률형 아이템도 이항 분포로 설명이 가능하다. 우선 이항 분포로 설명하고, 뒤에서 다항 분포로 설명을 확장한다.
예를 들어, 아래와 같은 획득 확률을 갖는 확률형 아이템이 있다고 가정하자. 확률형 아이템을 구매하면 A부터 I까지 총 9개의 아이템 중에서 하나가 각각 정해진 확률에 의해서 나타난다.
| 아이템 | 획득 확률 |
|---|---|
| A | 0.1% |
| B | 0.5% |
| C | 3.4% |
| D | 5.0% |
| E | 10.0% |
| F | 12.0% |
| G | 19.0% |
| H | 20.0% |
| I | 30.0% |
역시나 플레이어가 원하는 아이템은 A다. 0.1%의 획득 확률로 아이템 A를 얻으면 ‘성공’이고, 나머지 아이템을 얻으면 ‘실패’라고 정의한다. 이러한 경우, 확률형 아이템을 구매해서 결과를 확인하는 과정은 성공 확률이 0.1%인 베르누이 시행(Bernoulli trial)이 된다.
| 아이템 | 획득 확률 |
|---|---|
| A(success) | 0.1% |
| Others(fail) | 99.9% |
성공 확률이 $p$인 베르누이 시행을 $n$번 반복했을 때, $k$번 성공할 확률은 이항 분포(binomial distribution)를 따른다. 단순하게 생각하면, 아이템 A가 나올 확률이 0.1%이므로 확률형 아이템 1,000개를 구매하면 아이템 A를 한 개 얻을 수 있다. 그러나 실제로 1,000개의 확률형 아이템을 구매했을 때, 아이템 A가 1개 나올 확률($= P(X=1)$)은 약 36.8%다. 확률 계산은 아래와 같이 R을 이용한다.
> dbinom(1, 1000, .001)
[1] 0.36806351,000개의 확률형 아이템을 구매했을 때, 아이템 A를 한 개도 얻지 못 할 확률($= P(X=0)$)도 약 36.8%다. 즉, 100명의 플레이어가 1,000개의 확률형 아이템을 각각 구매했을 때, 36명은 아이템 A를 얻지 못한다.
> dbinom(0, 1000, .001)
[1] 0.36769541,000개의 확률형 아이템을 구매했을 때, 얻을 수 있는 아이템 A의 개수에 따른 확률 분포는 아래와 같다. 1,000개의 확률형 아이템을 구매하더라도 5개 이상의 아이템 A를 얻을 확률은 1% 미만이다.
> plot(0:10, dbinom(0:10, 1000, .001),
+ type='h',
+ xlab='success',
+ ylab='probability')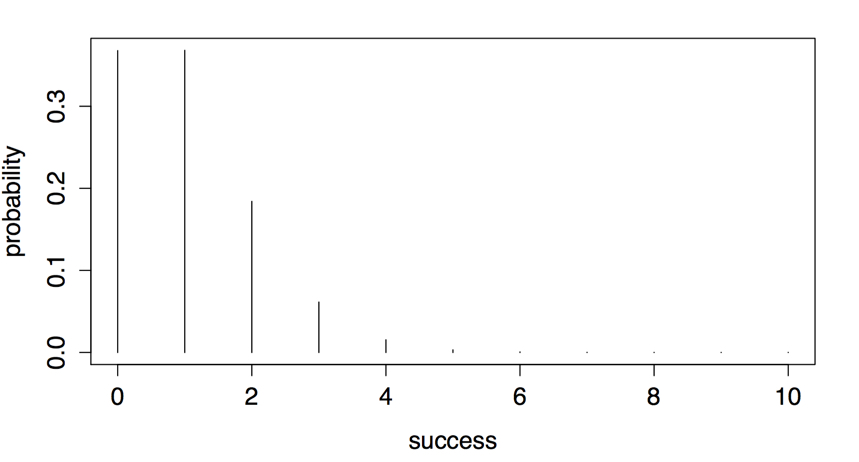
몇 개의 확률형 아이템을 구매해야 하나? - 음이항 분포
‘온라인 게임에서의 이항 분포’에서 살펴본 강화 성공 확률과 마찬가지로, 몇 번의 시행을 해야만 원하는 성공 횟수를 달성할 수 있는지가 궁금하다. 위에서 살펴 본 확률형 아이템을 몇 개 구매하면 아이템 A를 상당히 높은 확률로 구할 수 있을까? 이에 대한 확률을 구하려면 음이항 분포(negative binomial distribution)를 활용한다. 이는 목표한 성공 횟수에 도달하기 위해서 얼마나 많은 실패가 필요한지 실패 횟수 $r$에 대한 확률을 계산한다.
한 번의 성공을 위해서 필요한 시도 횟수에 대한 확률 분포를 그림으로 나타내면 아래와 같다.
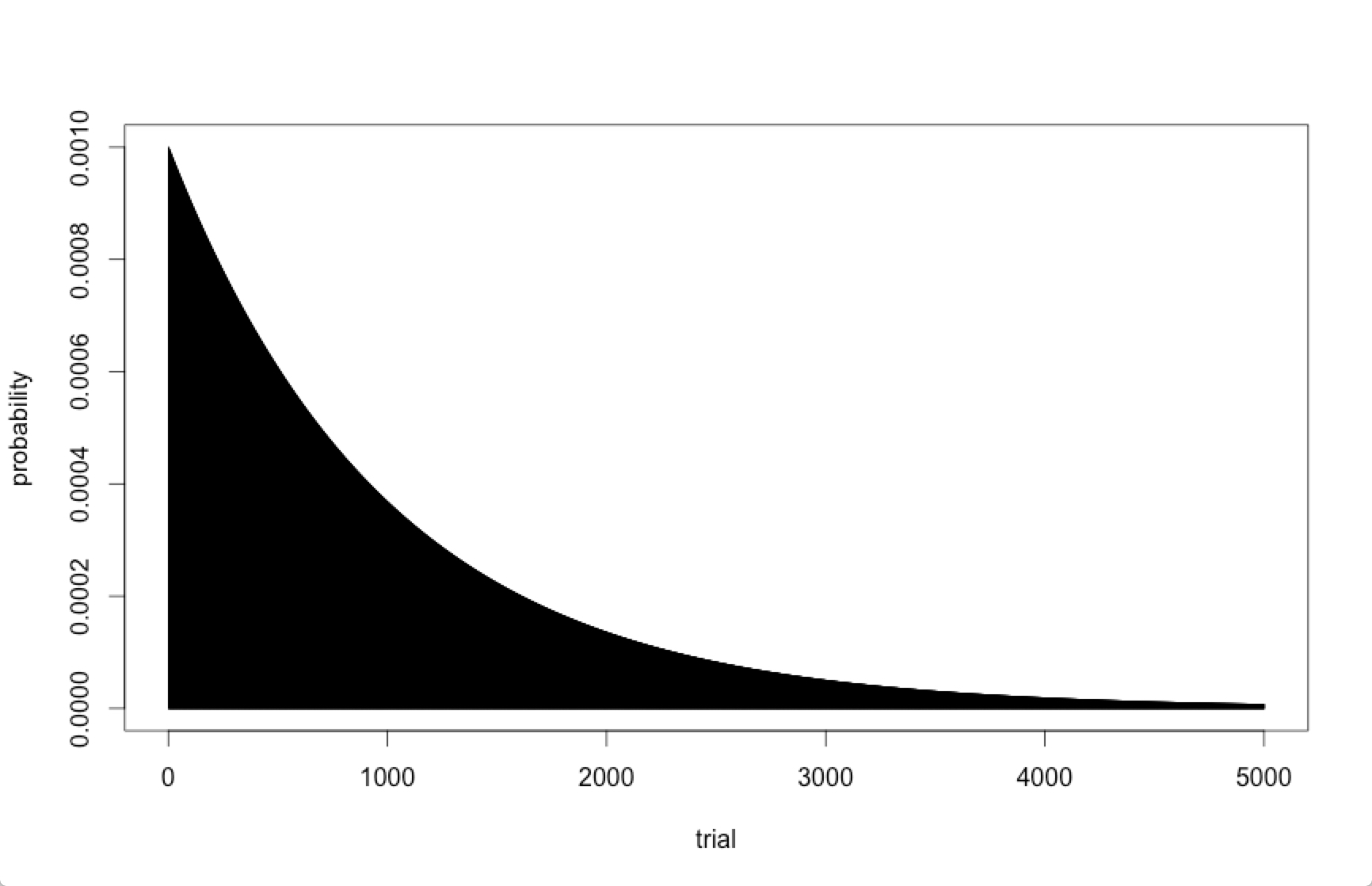
해당 확률을 누적해서 표현하면 아래와 같다. 대략 1,000개의 확률형 아이템을 구매해야 현실적인 확률에 도달할 수 있는 것을 알 수 있다.
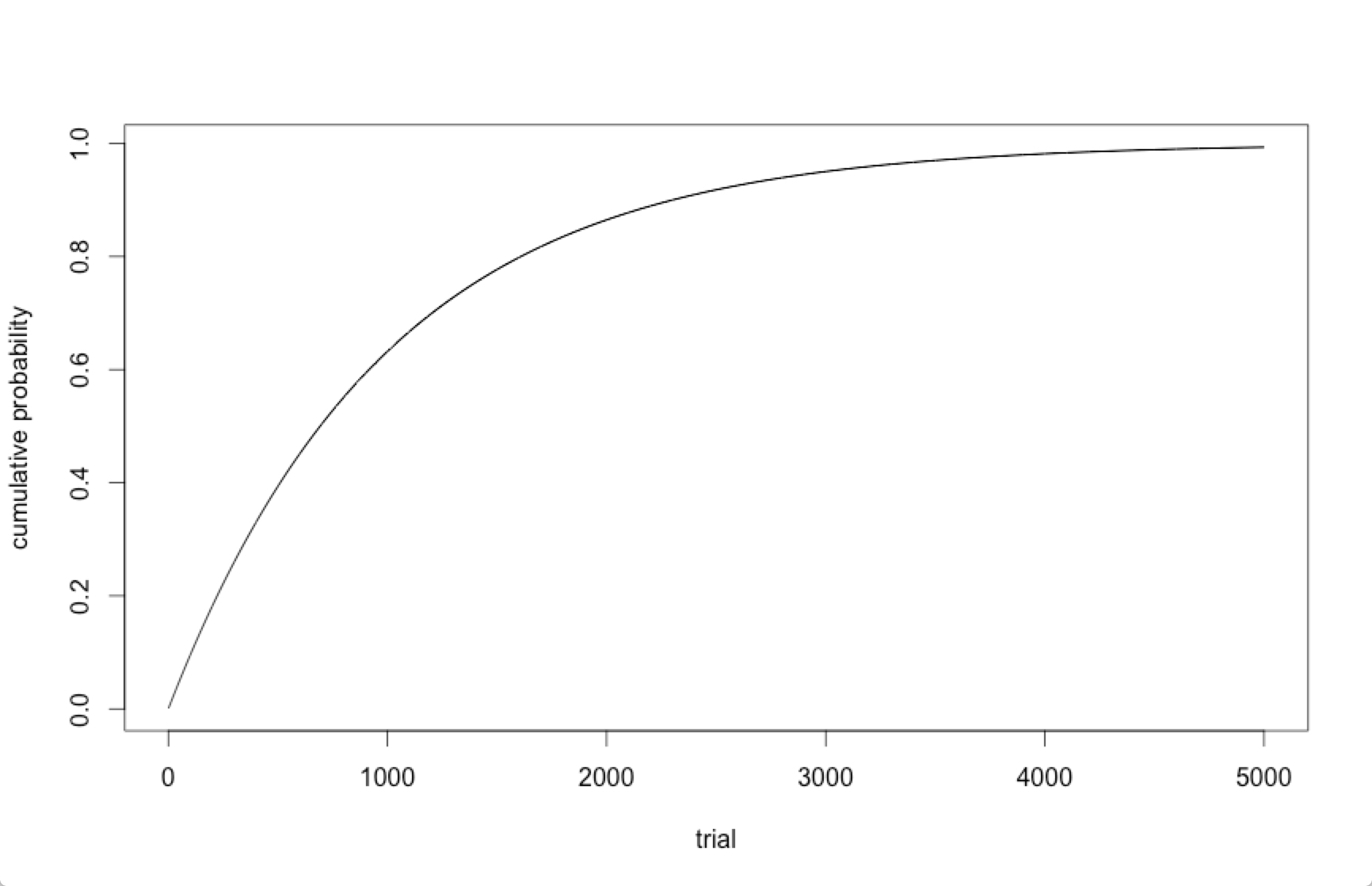
1,000개의 확률형 아이템을 구매해서 아이템 A를 얻을 확률을 계산해보면 약 63%다. 0.001%의 획득 확률을 그대로 해석하면 1,000번 시도해서 한 번 성공한다는 의미지만, 실제로 1,000개의 확률형 아이템을 구매해도, 37%의 플레이어는 원하는 아이템을 얻지 못한다.
> pnbinom(999, 1, .001)
[1] 0.6323046아이템 A를 한 개 얻을 확률 50%를 보장하려면, 693개의 확률형 아이템을 구매해야 한다. 반대로 말하면, 모든 플레이어가 693개의 확률형 아이템을 구매해도 절반의 플레이어는 아이템 A를 얻지 못한다.
> qnbinom(.5, 1, .001)
[1] 69295%의 확률로 아이템 A를 갖기 위해서는 2,995개의 확률형 아이템을 구매해야 한다. 99%의 확률을 보장받으려면 4,603개의 확률형 아이템을 구매해야 한다.
> qnbinom(.95, 1, .001)
[1] 2994
> qnbinom(.99, 1, .001)
[1] 4602당연히, 억세게 운이 나쁜 플레이어도 존재하기 때문에 100% 아이템 A를 보장받는 실패 횟수는 없다.
> qnbinom(1.0, 1, .001)
[1] Inf확률형 아이템의 획득 확률 - 다항분포
확률형 아이템의 결과를 단순화시켜서 이항분포로 설명하였다. 이를 단순화시키지 않고 그대로 사용하여 확률을 계산하기 위해서는 이항분포가 아니라 다항분포를 사용한다. 다항분포(multinomial distribution)는 시행의 결과가 2개를 초과하는 시행을 n번 반복하여 k번 성공하는 경우의 확률을 계산한다. 결과가 단 두 개일 때는 ‘k번 성공’으로 결과를 요약할 수 있으나, 결과가 2개를 초과하므로 시행 결과는 좀 더 복잡해진다.
예를 들어, A부터 I까지의 아이템이 나오는 확률형 아이템을 1,000개 구매한다면 이에 대한 결과는 각 아이템을 몇 개 얻었는지로 표현할 수 있다. 아래는 이런 사건 중에 하나다. 즉, 1,000개의 확률형 아이템을 구매한다면 거기서 얻는 아이템은 총 1,000개 되며, 그 종류는 9개 중 하나가 된다.
| A | B | C | D | E | F | G | H | I | total |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 7 | 35 | 50 | 112 | 106 | 183 | 208 | 299 | 1,000 |
위에 예시를 든 사건은 수 많은 가능한 조합 중에 하나다. 즉, 가능한 결과가 9개나 되기 때문에 가능한 사건은 무수하게 많다. 실제로 위에 예로 든 사건이 일어날 확률을 구하면 0.00000000004986008가 된다.
> dmultinom(c(0, 7, 35, 50, 112, 106, 183, 208, 299), prob=c(.001, .005, .034, .05, .1, .12, .19, .2, .3))
[1] 0.00000000004986008확률 값이 이렇게 작은 이유는 무수히 많은 사건 중 특정 사건 하나의 확률을 구했기 때문이다. 결과가 많을수록 이런 현상은 두드러지며, 실질적으로 단일 사건의 확률을 구하는 것은 무의미하다.
동일한 사건에서 아이템 A와 B에만 관심이 있다면 위의 사건은 아래와 같이 단순화할 수 있다.
| A | B | others | total |
|---|---|---|---|
| 0 | 7 | 993 | 1,000 |
> dmultinom(c(0, 7, 993), prob=c(.001, .005, .994))
[1] 0.03853889즉, 확률형 아이템을 1,000개 구매하여 아이템 A는 0개, 아이템 B는 7개 얻을 확률은 약 3.85%다. 나머지 아이템을 몇 개 얻는지는 큰 관심이 없다.
만약, 아이템 A에 대해서만 관심이 있다면 사건은 아래처럼 단순해진다.
| A | others | total |
|---|---|---|
| 0 | 1,000 | 1,000 |
> dmultinom(c(0, 1000), prob=c(.001, .999))
[1] 0.3676954즉, 1,000개의 확률형 아이템을 구매했을 때 아이템 A를 하나도 얻지 못할 확률은 약 36.8%다. 그런데 이는 이항사건과 같다. 따라서 아래와 같이 이항분포를 이용해서도 같은 확률을 얻을 수 있다.
> dbinom(0, 1000, .001)
[1] 0.3676954가능한 결과가 많은 시행의 경우, 관심의 대상이 한정적인 경우가 많다. 위와 같이 시행을 단순화시키는 것이 플레이어의 경험을 상상하는데 도움이 된다.
이항분포가 다항분포로 확장되는 것과 마찬가지로 음이항분포는 음다항분포(negative multinomial distribution)로 확장된다. 그러나 확률형 아이템에 따른 플레이어의 경험을 가늠하는데 크게 유용하지 않고, 계산이 복잡하여 생략한다. (R에 함수가 없다.) 특별히 관심이 있다면 글에 첨부한 링크를 활용한다.
복잡한 문제 단순화 하기
확률형 아이템의 확률은 다항분포를 활용하여 계산하는 것이 맞지만, 이항분포 문제로 단순화시키는 것이 훨씬 직관적이며 현실에 유용하다. 혹은, 확률형 아이템의 결과를 임의의 등급으로 나누어 계산하는 것이 편리하다. 가능한 모든 결과의 조합으로 확률을 구하는 과정은 불필요한 경우가 많다. 특히, 확률형 아이템에서 관심의 대상이 되는 결과는 극히 일부다. 굳이 ‘꽝’을 신경써야 하는 경우는 많지 않다.
비단 확률형 아이템 문제가 아니더라도 게임 속에서 상당히 많은 사건이 다항분포 문제에 해당한다. 결과의 가짓수가 많다면 먼저 문제를 단순화시켜서 살펴보고 점차 복잡하게 확장하는 것이 유용하다.
