신뢰 구간을 이용한 A/B 테스트 결과 비교
신뢰 구간 계산만으로 A/B 테스트 결과를 빠르게 비교할 수 있는 방법에 대해 소개한다.
A/B 테스트에 대한 기본적인 소개는 ‘A/B 테스팅이란’ 글을 참고한다.
간단한 웹사이트의 예시
가장 간단한 A/B 테스팅을 다음과 같이 생각할 수 있다. 방문객은 무작위로 Variation A 또는 Variation B에 할당된다. Variation A에 할당된 방문객은 특정 화면에 노출되고, Variation B에 할당된 방문객은 또 다른 특정 화면에 노출된다.
실험의 목표는 과연 어떤 화면에 노출되었을 때 방문객이 더 많은 구매를 하는지 알아보는 것이다. 이를 위해 방문객 당 평균 구매액(Average Purchase Per Visitor)을 계산하고 비교한다. 약 1주일의 실험 결과 아래와 같은 결과를 얻었다.
| variation | # Unique Visitors | Sum of Purchases | APPV |
|---|---|---|---|
| Variation A | 100,123 | 14,023,000 | 140.06 |
| Variation B | 100,523 | 22,102,000 | 219.87 |
실험 결과를 보면 Variation B의 효과가 극명하게 높다. 평균 방문객마다 219.87원($= 22102000 \div 100523$)의 구매액을 보이고 있다. 당장 Variation B를 채택하지 않을 이유가 없다.
문제는 실험의 결과 차이가 항상 극명하게 갈리지 않는다는 점이다. 위의 예시에서 만약 Variation B의 평균 구매액이 142원으로 계산된다면 방문객을 어느 화면에 노출시키는 것이 좋다고 쉽게 결론 내리기 어렵다. 게다가 운이 좋아서 특정 Variation의 결과가 일시적으로 좋을 것이라는 걱정도 떨칠 수가 없다.
점 추정
위의 실험 예시에서 문제는 평균 구매액의 점 추정(point estimation)만으로 실험 결과를 비교한다는 점이다. 점 추정에 대해서 설명하기 전에 무엇을 왜 추정하는지 알 필요가 있는데, 추정이라는 것은 불확실한 무엇을 알기 위한 과정이다. 위 실험에서 알고 싶은 불확실한 무엇은 모집단의 평균 구매액이다. 1주일의 실험을 하는 동안 약 20만명의 방문객이 실험에 참여하였지만, 실험을 하는 마케터는 앞으로 방문할 모든 방문객의 평균 구매액이 알고 싶다. 1주일 동안 실험에 참여한 방문객들은 표본 집단이며 이들의 평균 구매액은 표본 평균이 된다. 모집단의 평균(모평균) 값을 알기 위해서 표본 평균을 활용하는데, 단 하나의 값으로 이를 추정하는 과정이 점 추정이다. 따라서 평균 표본은 모평균의 점 추정 값이다.
앞으로 방문할 모든 방문객의 평균 구매액은 실험을 아무리 반복해도 알 수 없다. 만약 알 수 있다고 하더라도, 시간이 흐른 후에 이 값을 정확하게 아는 것은 실무에서 별 소용이 없다. 실험에서 얻은 데이터를 최대한 활용해서 현재 선택할 수 있는 가장 좋은 의사 결정을 내리는 것이 중요하다. 아직 사용하지 않은 데이터는 실험 데이터의 분산 값이다. 이를 활용하여 평균 구매액의 점 추정 값이 아니라 구간 추정 값을 계산한다.
구간 추정
표준 오차
실험을 할 때마다 우연이 개입하여 표본 평균은 달라질 수 있다. 위의 실험 예시에서 보면, 다른 1주일 동안 실험을 할 경우에는 다른 평균 구매액이 나타날 수 있다. 모든 실험이 표본 집단을 토대로 수행되므로 표본 평균이 실험마다 조금씩 달라지는 것은 어쩔 수 없는 현상이다. 문제 해결의 핵심은 매번 움직이는 표본 평균을 탓할 것이 아니라 얼마나 많이 움직이는지를 평가하는 것이다. 표본 평균의 변동성은 표본 분산과 표본 집단의 크기로 알 수 있는데 이를 표준 오차(standard error)라고 한다.
표본 평균의 표준 오차는 아래와 같다.
\[SE_{\bar{x}} = \frac{s}{\sqrt{n}}\]- $s$: 표본 표준 편차
- $n$: 표본 크기
만약 Variation A에 할당된 방문객이 100,123명이고 표본 표준 편차가 3,102 라면 표본 오차는 아래와 같다.
\[SE_{\bar{x}_{A}} = \frac{s_{A}}{\sqrt{n_{A}}} = \frac{3102}{\sqrt{100123}} = 9.80\]신뢰 구간 (Confidence Interval)
표본 평균의 확률 분포는 표본 크기가 충분히 큰 경우에 정규 분포를 따르게 되는데, 이는 중심 극한 정리(central limit theorem)에 의해 증명된다. 중심 극한 정리는 본 글의 범위를 넘어서므로, 설명은 생략한다. 핵심은 표본 평균의 값과 표준 오차를 알면 정규 분포를 이용하여 표본 평균의 범위를 구할 수 있다는 점이다.
위의 표본 오차를 토대로 Variation A에 대한 표본 평균의 95% 신뢰 구간(confidence interval)을 구하면 아래와 같다.
\[\begin{align} \bar{x}_{A} \pm 1.96 \times SE_{\bar{x}_{A}} & = 140.96 \pm 1.96 \times 9.80 \\ & = (120.85, 159.27) \end{align}\]1.96은 표준 정규 분포에서 97.5 백분위 수에 해당하는 숫자다. 아래 그림처럼 $\pm 1.96$ 사이에 표준 정규 분포의 95% 영역이 포함된다.

<그림 출처: https://en.wikipedia.org/wiki/1.96>
Variation A의 평균 구매액에 대한 95% 신뢰 구간이 $(121.75, 160.17)$로 나타났는데, 이는 여러 개의 다른 표본에서 신뢰 구간을 같은 방법으로 구할 경우 95%의 구간들이 모평균을 포함한다는 의미다. 간단하게는 해당 범위를 통하여 표본 평균의 범위가 대략 어느 정도인지 알 수 있다. 점 추정과 비교하면, 단순히 점 하나로는 알 수 없는 표본 평균의 변동성을 알 수 있기 때문에 다른 표본과의 비교가 용이하다.
2개 표본에 대한 신뢰 구간 비교
Variation A에 대해서 계산한 것과 마찬가지로 Variation B의 표준 오차와 95% 신뢰 구간을 아래와 같이 구할 수 있다.
\[SE_{\bar{x}_{B}} = \frac{s_{B}}{\sqrt{n_{B}}} = \frac{3923}{\sqrt{100523}} = 12.37\] \[\begin{align} \bar{x}_{B} \pm 1.96 \times SE_{\bar{x}_{B}} & = 219.87 \pm 1.96 \times 12.37 \\ & = (195.62, 244.12) \end{align}\]| variation | # Unique Visitors | Sum of Purchases | APPV | std of Purchases | 95% CI |
|---|---|---|---|---|---|
| Variation A | 100,123 | 14,023,000 | 140.06 | 3,102 | (120.85, 159.27) |
| Variation B | 100,523 | 22,102,000 | 219.87 | 3,923 | (195.62, 244.12) |
두 표본 평균의 신뢰 구간을 비교하면 아래 그림과 같다.
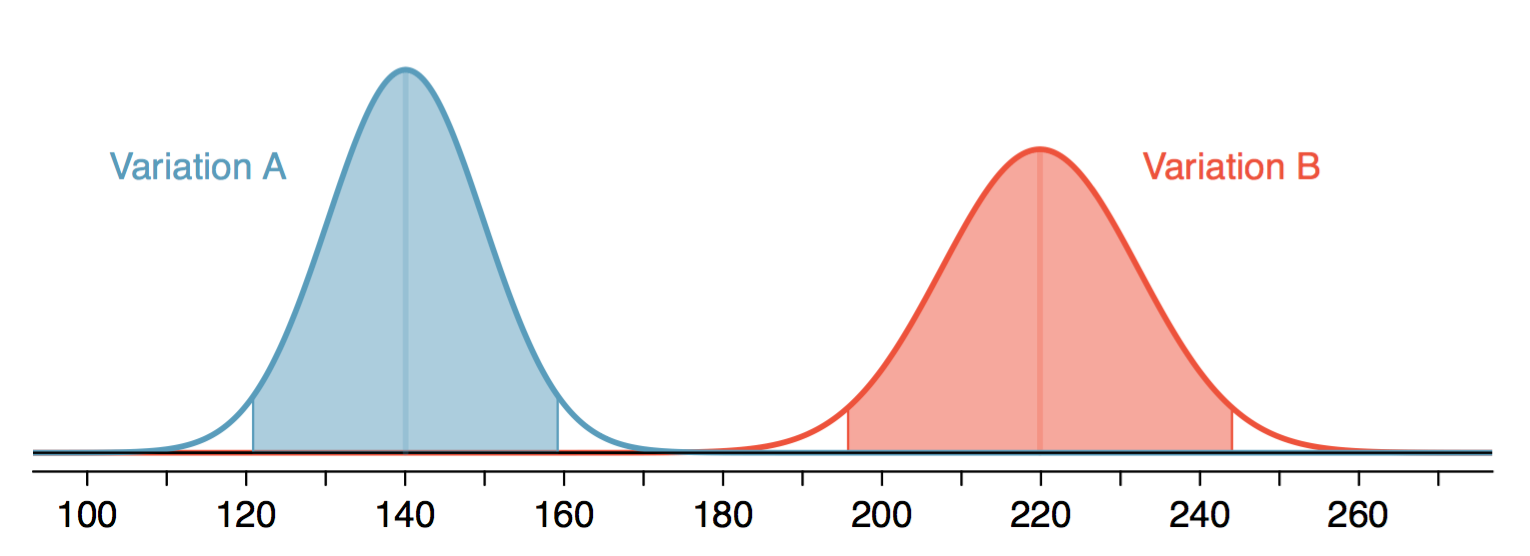
각 Variation의 신뢰 구간이 겹치지 않는 것을 알 수 있다. 이와 같이 각 신뢰 구간이 겹치지 않는 경우, 두 표본 평균은 유의하게 다르다(significantly different). A/B 테스트 결과로 이야기하면, B의 평균 구매액이 A의 평균 구매액보다 크다.
주의할 것은 그 역은 성립하지 않는다는 점이다. 신뢰 구간이 겹치지 않는다면 두 표본 평균은 유의하게 다르다고 할 수 있지만, 신뢰 구간이 겹치는 경우에는 그 정도에 따라서 표본 평균이 유의하게 다르거나 다르지 않을 수 있다. 그렇다면 왜 신뢰 구간으로 표본 평균을 비교할까?
신뢰 구간을 계산하는 것은 비교적 직관적이며 쉽다. 2개의 표본 평균이 일정한 범위를 가지며, 그 범위가 겹치지 않으면 서로 유의하게 다르다는 것은 빠르게 이해 가능하다. 게다가 신뢰 구간만 계산하고 눈으로 기본적인 결과 비교가 가능하다. 만약 신뢰 구간이 겹친다면 가설 검정을 제대로 할 필요가 있다. 신뢰 구간을 이용한 통계적 유의성 검토는 빠르지만 정확하지 않은 방법이다. 전형적인 가설 검정에 대해서는 더 좋은 참고서들이 많으니 이 글에서는 생략한다.
겹치는 신뢰 구간(overlapping CI)
(참고1 - Overlapping Confidence Intervals and Statistical Significance)
(참고2 - If we’re so different, why do we keep overlapping?)
왜 신뢰 구간이 겹칠 때에도 통계적으로 유의미한 차이가 있을 수 있을까? 95% 신뢰 구간 2개를 비교하면, 유의 수준 5%의 가설 검정이 자연스럽게 성립한다고 오해하기 쉽지만, 그렇지 않다. 만약 2개의 표본 평균의 신뢰 구간이 겹치지 않는다면 두 표본 평균은 유의하게 다르다.(significantly different) 그러나 2개의 신뢰 구간이 겹친다면 두 표본 평균은 유의하게 다르거나 혹은 다르지 않다.
이러한 예시를 만드는 것은 쉬우므로 생략하고 원인을 설명하자면, 이는 가설 검정을 할 때와 신뢰 구간을 계산할 때 사용하는 표준 오차가 다르기 때문이다. 일반적인 가설 검정에서는 차이의 표준 오차(standard error of difference)를 사용하지만, 신뢰 구간을 계산할 때는 각각의 표준 오차를 따로 사용한다.
A/B 테스트 예시를 다시 사용하면, 가설 검정에서는 아래와 같은 경우 두 표본 평균이 유의하게 다르다고 판단한다.
\[(\bar{x}_B - \bar{x}_A) - 1.96 \times \sqrt{SE_{A}^2 + SE_{B}^2} > 0 \qquad (1)\]그러나 두 평균의 신뢰 구간을 비교하는 경우에는 아래와 같은 경우에 신뢰 구간이 겹치지 않는다.
\[\bar{x}_B - 1.96 \times SE_{B} > \bar{x}_A + 1.96 \times SE_{A}\] \[(\bar{x}_B - \bar{x}_A) - 1.96 \times (SE_{A} + SE_{B}) > 0 \qquad (2)\]모든 양수에 대해서 아래의 조건이 성립하므로,
\[SE_{A} + SE_{B} > \sqrt{SE_{A}^2 + SE_{B}^2}\]조건 $(2)$가 성립할 때는 항상 조건 $(1)$이 성립한다. 그러나 조건 $(2)$가 성립하지 않는 경우에도, 조건 $(1)$은 성립할 수 있다. 따라서 신뢰 구간이 겹치지 않을 때는 항상 통계적으로 유의하게 다르다는 결론을 내릴 수 있지만, 그렇지 않을 경우에는 결론을 내릴 수 없다.
그리고 이를 토대로 알 수 있는 것은 95% 신뢰 구간이 겹치지 않는다는 것이 5% 유의 수준 하의 가설 검정보다 더 엄격한 기준이라는 점이다. 따라서 신뢰 구간이 겹치지 않는 경우에는 통계적 유의성에 대해서 빠르게 판단 가능하다.
결론
A/B 테스트 결과를 빠르게 비교할 수 있는 방법으로 신뢰 구간을 활용할 수 있다. 특히, 표본 평균의 신뢰 구간이 겹치지 않는다면 통계적으로 유의한 차이가 있다고 본다. 그러나 이는 빠르게 결과를 확인하는 용도이지 결코 가설 검정을 대체할 수는 없다. 실무에서 유용하므로 잘 이해하고 쓰는 것을 추천한다.
앞으로 더 이야기할 문제
A/B 테스트의 결과를 잘 분석하기 위해서는 더 고려해야할 것이 많다. 특히, 샘플 사이즈와 검정력(power), 효과 크기(effect size)를 이해하는 것이 매우 중요하다. 이를 제대로 알아야 맹목적으로 p-value에만 의지하는 결과 해석을 피할 수 있다.
가설 검정과 더불어서 A/B 테스트는 변하는 세상에 대응하기 위한 노력이 수반되어야 한다. 기존의 실험 환경과는 다르게 시시각각 변하는 환경에서 실험을 수행하기 때문에 이에 대비한 장치가 필요하다. MAB나 Bayesian A/B test가 좋은 대안이다.
