A/B 테스트에서 p-value에 휘둘리지 않기
A/B 테스트 결과 분석은 주로 빈도주의 관점에서 유의성 검정(NHST)을 따른다. 문제는 유독 유의 확률(p-value)에만 신경을 쓰느라 제대로 실험 결과를 해석하지 않는다는 점이다. 실험의 목적은 얼마나 효과가 있는지 살펴보는 것이지 통계적 유의성(statistical significance)만을 확보하는 것이 아니다.
p-value란?
p-value가 무엇을 의미하는지 알아야 이것에 매몰되지 않는다. A/B 테스트에서는 마냥 p-value가 작아질 때까지 실험 결과를 모니터링하면서 기다리는 경우가 많다. 우선 p-value < 0.05가 무슨 뜻인지 이해해야 왜 실험 기간을 무한정 늘릴 필요가 없고, 실험을 너무 일찍 끝내서도 안된다는 점을 알 수 있다.
가설 검정
흔한 A/B 테스트를 생각해보자. Variation A와 B의 전환율(conversion rate)을 각각 $p_{A}$, $p_{B}$라고 한다면, 귀무 가설($H_{0}$: null hypothesis)과 대립 가설($H_{1}$: alternative hypothesis)은 아래와 같다. 편의상 단측 검정을 염두에 둔다.
\[\begin{align} H_{0}: & \; d = p_{A} - p_{B} = 0 \\ H_{1}: & \; d > 0 \end{align}\]유의성 검정은 위의 두 가지 가설 중에서 귀무 가설을 기본 전제로 삼는다. 아주 강력한 증거가 없다면, 일단 실험 결과에 효과가 없다고 가정한다. 마치 법정에서 강력한 증거가 없다면 무죄 추정의 원칙을 적용하는 것과 같다.
두 가지 오류
실험을 진행하면서 얻게 되는 데이터에 근거하여 귀무 가설을 기각할 것인지 결정한다. 문제는 실험을 수행하여도 귀무 가설을 기각할 것인지 말 것인지 완벽하게 결정할 수 없다는 점이다. 실험 결과는 표본에서 얻은 데이터이기 때문에 항상 오차가 생긴다. 즉, 항상 오류를 범할 가능성이 존재한다.
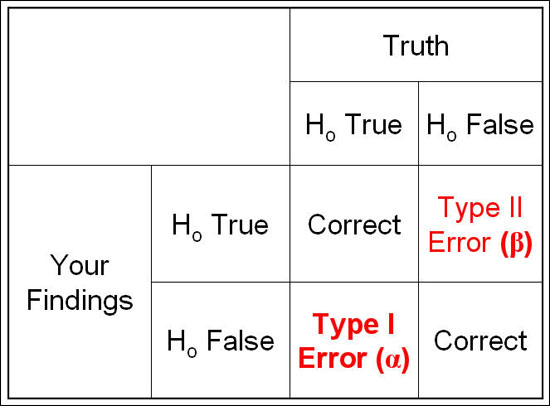
<그림 출처: http://epiville.ccnmtl.columbia.edu/popup/power_and_sample_size_introduction.html>
- Type I Error: 1종 오류, 귀무가설이 사실인데 기각할 오류
- Type II Error: 2종 오류, 귀무가설이 거짓인데 기각하지 않을 오류
곧이 곧대로 읽으면, 참 이해하기 어렵다. 좀 더 쉽게 풀어 쓰면 다음과 같다.
- 우리는 효과가 있는지 없는지 찾기 위해 실험을 한다.
- (효과가) 없는데 있다고 할 오류 = 1종 오류
- (효과가) 있는데 없다고 할 오류 = 2종 오류

<그림 출처: http://flowingdata.com/2014/05/09/type-i-and-ii-errors-simplified/>
오류 수준 정하기
‘없는데 있다고 할 오류’가 더 위험할까? ‘있는데 없다고 할 오류’가 더 위험할까? 일반적으로 ‘없는데 있다고 할 오류’를 더 위험하게 본다. 과학적 증거를 발견하려는 실험에서 실제로 없는 증거를 있다고 오해하는 경우에 생길 위험성을 경계하기 때문이다. 게다가 사람은 패턴을 발견하는데 비상한 재주를 가지고 있다. 없는 무언가를 있다고 결론 내리는 경우가 많다. 이를 방지 하기 위해서도 ‘없는데 있다고 할 오류’를 상대적으로 더 경계하는 것이 좋다.
<”Face of Mars”. 그림 출처: https://en.wikipedia.org/wiki/Cydonia_(region_of_Mars)>
물론 이는 경우에 따라서 다를 수 있다. 어떤 오류를 범하는 것이 더 위험한지는 실험에 따라 다르다. 만약 암 환자를 진단하기 위한 실험을 한다면, ‘(암이) 없는데 있다’고 하는 것이 ‘(암이) 있는데 없다’고 하는 것보다 낫다. 암이 없는데 있다고 오진하면 더 비싼 검사를 받고 정확한 진단을 받을 기회가 있지만, 암이 있는데 없다고 오진하면 조기 치료를 받을 기회를 잃게 된다.
일반적으로 1종 오류에 대한 기준은 5%다. 없는데 있다고 할 오류 수준을 5%로 제약한다. p-value < 0.05에서 0.05는 여기서 나왔다.
p-value 구하기
지금까지의 모든 논의는 실제로 실험을 수행하기 전에 이루어진다. 아직 아무런 데이터도 없고 그저 실험을 설계만 했다. A/B 테스트를 할 예정이고, 두 실험군의 전환율(CR) 차이가 있는지 없는지 가설 검정을 할 예정이다. ‘차이가 없는데 있다고 할 오류’ 수준은 0.05로 실험 전에 정했다.
실제로 실험을 한 결과가 아래와 같다고 하자.
| Variation | Trial | Conversion | Conversion Rate |
|---|---|---|---|
| Variation A | 109,925 | 14,517 | 0.1321 |
| Variation B | 110,402 | 14,291 | 0.1294 |
이를 근거로 귀무 가설의 확률 분포를 그리면 아래와 같다.
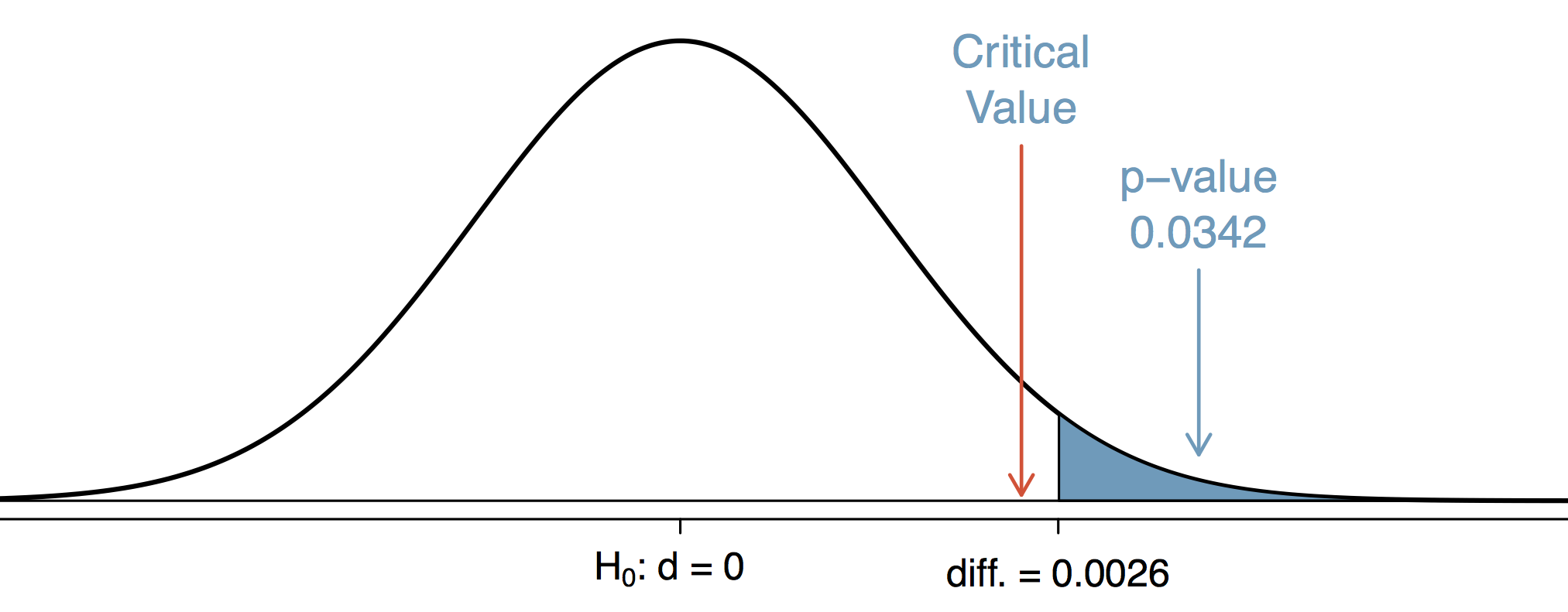
일단 왜 귀무 가설에 해당하는 분포만 그렸는지 이해하는 것이 중요하다. 유의성 검정에서는 일단 귀무 가설이 맞다고 본다. 무죄 추정의 원칙이다. 귀무 가설은 차이가 0임을 가르키므로 확률 분포의 중심은 0이다. 분포의 분산은 실험 데이터를 이용해 추정한다. 여기서는 편의상 정규 분포를 사용한다.
p-value를 귀무 가설 확률 분포에서 구한다는 점이 중요하다. p-value는 귀무 가설이 맞다는 무죄 추정의 원칙 하에서 계산한 값이다. 즉, 귀무 가설이 맞다는 가정하에서 실험 데이터가 나올 확률을 의미한다. 이를 조건부 확률로 나타내면 아래와 같다.
\[P(D|H_0) = 0.0342\]귀무 가설이 맞다는 가정 하에서 이런 실험 데이터가 관찰될 확률은 ‘없는데 있다고 할 오류’ 수준($= 0.05$)보다 낮다. 즉, 미리 설정한 1종 오류의 허용 한계보다 이러한 데이터가 관찰될 확률이 더 낮다. 귀무 가설이 맞다는 가정하에서는 정말 나오기 힘든 실험 데이터가 나온 것이다. 따라서 두 실험군 사이에 차이가 없다는 귀무 가설을 기각한다. 전형적인 유의성 검정 방법이다. 이제 통계적으로 유의한 차이(statistically significant difference)가 있다고 보고서에 쓴다.
유의하지 않은 실험 결과
실험 결과를 조금 바꿔서 아래와 같은 결과를 얻었다고 가정하자.
| Variation | Trial | Conversion | Conversion Rate |
|---|---|---|---|
| Variation A | 109,925 | 14,517 | 0.1321 |
| Variation B | 110,402 | 14,391 | 0.1304 |
이를 근거로 귀무 가설의 확률 분포를 그리면 아래와 같다.
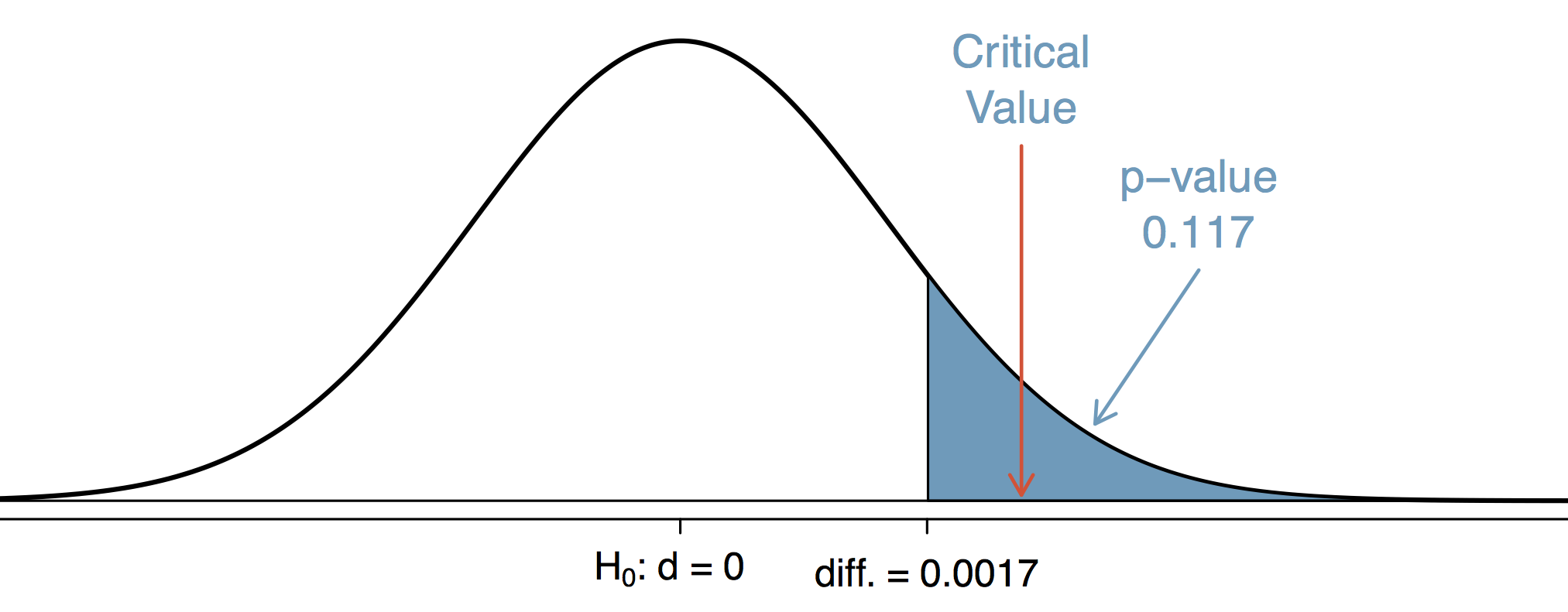
p-value가 0.117로 0.05보다 크다. 무죄추정의 원칙을 깨뜨리고, 죄가 있다고 판정할만큼 증거의 강도가 강하지 않다. 통계적으로 유의하게 차이가 있다고 할 수 없는 상황이다.
유의하지 않은 실험 결과를 안고 더 기다리기
이 상황에서 실험 담당자가 선택할 수 있는 선택은 두 가지인데, 여기서 실험을 그만두고 두 실험군 사이에 통계적으로 유의한 차이가 없다고 결론 내리거나, 실험을 더 지속시킨다. 실험실에서의 실험과 다르게 A/B 테스트는 실험 기간을 연장하여 표본 크기를 늘릴 수 있다. 통계적으로 유의한 차이가 없는 실험 결과를 얻었다고 보고하기 싫은 담당자는 ‘밑져야 본전’이라는 생각으로 실험 기간을 더 늘린다. 결국 아래와 같은 실험 결과를 얻게 되었다.
| Variation | Trial | Conversion | Conversion Rate |
|---|---|---|---|
| Variation A | 219,850 | 29,034 | 0.1321 |
| Variation B | 220,804 | 28,782 | 0.1304 |
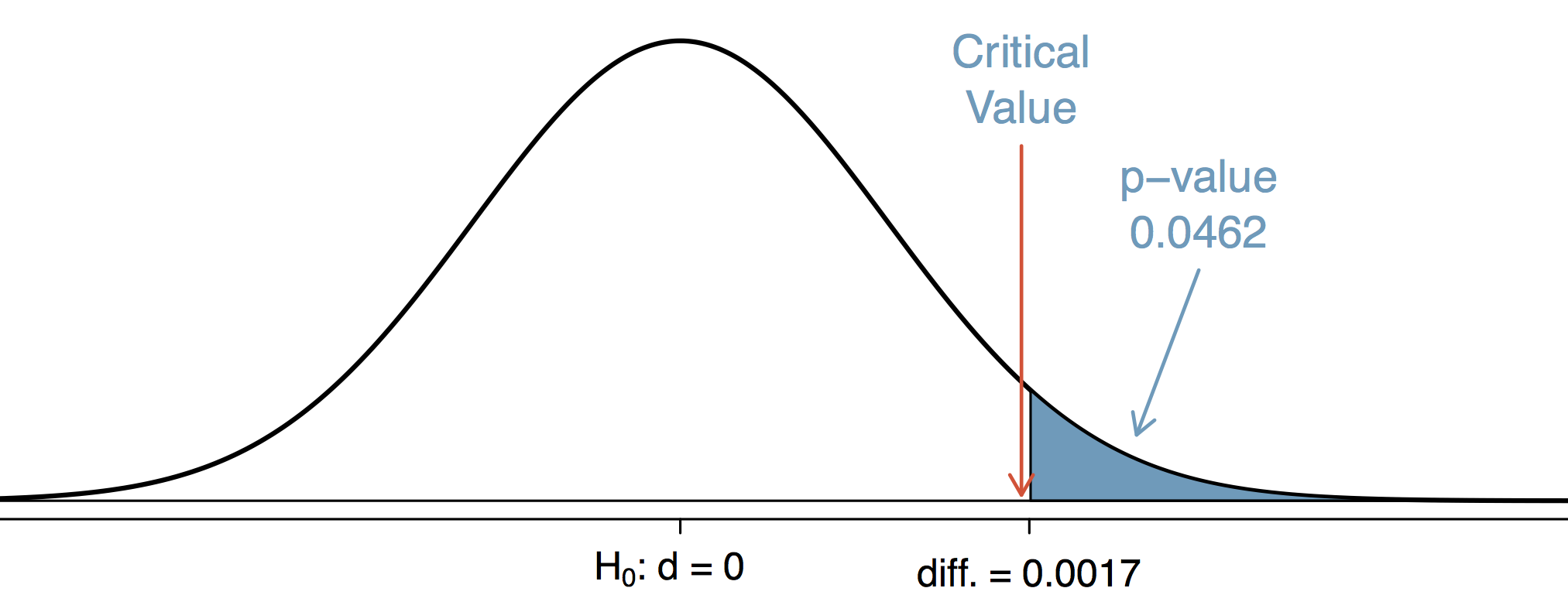
표본 크기가 커지면 표본 오차가 작아지고, 결과적으로 p-value가 작아질 가능성이 높다. 실험 기간을 늘리고 기다렸더니 실험 담당자에게 좋은 일이 생겼다. 통계적인 유의성을 확보하게 된 것이다. 이제 통계적으로 유의한 차이가 있다고 보고서에 쓴다.
여기서 재미있는 것은 통계적으로 유의한 실험과 그렇지 않은 실험 사이의 전환율 차이다. 아래 테이블은 통계적으로 유의한 차이가 없다고 결론 내린, 기다리기 전 실험 결과다.
| Variation | Trial | Conversion | Conversion Rate |
|---|---|---|---|
| Variation A | 109,925 | 14,517 | 0.1321 |
| Variation B | 110,402 | 14,391 | 0.1304 |
아래는 실험 기간을 연장한 결과다.
| Variation | Trial | Conversion | Conversion Rate |
|---|---|---|---|
| Variation A | 219,850 | 29,034 | 0.1321 |
| Variation B | 220,804 | 28,782 | 0.1304 |
두 실험 결과에서 전환율의 차이는 0.0017로 똑같다. 실제로 바뀐 것은 Trial과 Convesion의 값을 2배로 늘린 것 말고는 없다. 각 실험군의 전환율 값도 그대로 같다. 단순히 실험 기간이 늘어서 실험 규모가 커졌을 뿐이다.
문제 제기
몇 가지 궁금증이 생긴다.
- 두 실험군의 차이는 비슷해보이는데 통계적으로 유의한 차이를 얻으면 더 좋은 것인가?
- 실험자 마음대로 실험 기간을 늘려서 표본 크기를 임의로 키워도 되는가?
- 애초에 적절한 표본 크기라는 것이 있는가?
효과 크기를 무시한 유의성 검정
과연 “두 실험군의 차이는 비슷해보이는데 통계적으로 유의한 차이를 얻으면 더 좋을까?” 효과 크기(effect size)가 작다면, 아무리 통계적으로 유의한 차이가 있더라도 현실에서 큰 의미가 없다. 두 실험군 사이의 전환율 차이가 0.17%인 위의 예시로 돌아가 보자. 과연 현실에서 이 정도의 전환율 차이가 큰 의미를 가질까?
해당 실험을 하루 평균 구매 고객이 1000명인 홈페이지에서 했다고 가정하자. 0.17%의 전환율 상승이 가져오는 구매 고객 증가는 하루 평균 1.7명이다. 만약 구매 고객당 평균 매출액이 1만원이라면 0.17%의 전환율 상승은 평균적으로 하루에 17,000원 매출 상승을 의미한다.
같은 전환율 상승을 하루 평균 구매 고객이 100만 명인 회사에서 거둔다면 이야기는 달라진다. 0.17%의 전환율 상승은 하루 평균 1,700명의 추가 구매 고객을 의미하며, 1만원씩 구매를 한다면 하루에 1,700만원의 추가 매출이 생긴다.
중요한 것은 해당 효과가 현실에서 어느 정도의 가치를 의미하는지 아는 것이다. 0.1%의 전환율 상승이 중요하다면 해당 효과 크기에서의 유의성 확보는 매우 중요하다. 반대로 최소한 10%의 전환율 상승이 있어야 실험의 비용을 감당할 수 있는 상황이라면 0.17%의 효과에 대해서 유의성을 확보하기 위한 노력은 불필요하다.
위의 예시에서 본 것처럼, 실험 크기를 증가시키면 아주 작은 효과 크기에 대해서도 유의성을 확보할 수 있다. 즉, 없는데 있다고 판단할 오류를 배제할 수 있다. 하지만 아주 작은 효과 밖에 없다면, 과연 그 효과가 ‘없는데 있다고 판단할 오류’를 범하지 않기 위해 애쓸 필요가 있을까? 그 정도 차이는 있어도 소용 없으니 차라리 다른 실험을 준비하는 편이 낫다.
이 문제를 친구와의 키재기 내기로 비유하면 이렇다. 내 옆의 친구와 나의 키가 아주 비슷한데 내 생각에는 내가 확실히 더 큰 것 같다. 이를 증명하고자 1 마이크로 미터까지 계측이 가능한 자를 가져와서 나와 내 친구의 키를 측정한다. 결론적으로 10 마이크로 미터 만큼 내 키가 더 크다. 친구를 이겨서 기분은 좋을지 모르지만 시간 낭비하기에 참 좋은 일이다.
애초에 어떤 비교에서든 차이가 0일 가능성은 거의 없다. 얼마나 의미있는 계측 단위에서 차이가 있는지 없는지 구분하는 것이 중요하다.
적절한 표본 크기 정하기
그럼 실험 시작 전에 적절한 실험의 규모를 정할 수 있을까? 몇 가지를 미리 정하면 적절한 실험 규모를 알 수 있다. 1종 오류 수준과 2종 오류 수준, 그리고 탐지하고자 원하는 최소한의 효과 크기를 정하면 적절한 표본 크기를 계산할 수 있다. 지금까지 2종 오류에 대한 언급이 거의 없었는데, 실제로 많은 실험 담당자는 2종 오류에 대해서 전혀 신경쓰지 않는다.
1종 오류가 ‘없는데 있다고 판단할 오류’라면, 2종 오류는 ‘있는데 없다고 판단할 오류’다. 1종 오류를 유의 수준이라 말하고 이 오류의 한계를 보통 0.05라고 정한다. 2종 오류($=\beta$)는 바로 쓰지 않고, $1-\beta$ 값을 사용한다. 이는 ‘있는데 없다고 판단할 오류’의 여사건 개념이며, ‘(효과가) 있는데 있다고 판단할 능력’을 의미하기 때문에 검정력(power)이라고 부른다. 일반적으로 검정력은 0.8로 설정한다.
검정력이 0.8이라는 이야기는 탐지하려는 효과가 실제로 있을 때 효과가 있다고 판단할 가능성이 0.8이라는 의미다. 효과가 없는데 없다고 판단할 능력이 높은 것도 중요하지만, 실제로 효과가 있을 때 있다고 판단할 수 있는 능력도 중요하다. p-value는 효과가 없다는 가정 하에서 평가한 숫자다. 따라서 p-value와 별도로 검정력에 신경쓸 필요가 있다. 최악의 경우에는 원하는 효과 크기를 탐지할 가능성이 절반 이하인 실험 결과를 신뢰하고 중요한 의사 결정을 하게 될 수도 있다.
탐지하고자 원하는 최소한의 효과 크기는 실험마다 모두 다르다. 과학적 실험에서는 선행 연구를 참고하여 정하는 경우가 많다. 실무에서 A/B 테스트를 한다면 과연 얼마나 차이가 나야 이익인지 따져봐야 한다. 비슷한 실험을 한 사례가 있다면 이를 사용하는 것도 좋다.
적절한 검정력 계산기(power calculator)는 웹에 상당히 많다. 이 중에서 실험에 적절한 계산기를 선택해서 계산하면 된다. 대부분의 계산기들은 계산 방법에 대해 공개하고 있으므로 직접 코드로 구현해놓고 사용해도 좋다.
실험이 안 끝났는데 결과 살펴보기
실험의 유의성을 확보하기 위해서 실험 기간을 과하게 연장하는 경우도 문제지만, 반대로 실험이 끝나기도 전에 결과를 확인하고 이를 확신하는 경우도 문제다. 이를 실험 결과 엿보기(peeking) 문제라고 한다. 너무 일찍 실험을 멈추고 그 결과를 신뢰하는 경우인데, 실험 기간을 연장하는 것보다 더 큰 문제가 있다.
전형적인 실험 담당자는 시간날 때마다 실험 결과를 엿보면서 p-value를 확인한다. 그러다가 우연히도 p-value가 0.05보다 작아지는 순간을 포착해서 “드디어 실험이 끝났다”고 선언하고 실험을 마무리한다. 만약 충분한 표본 크기가 확보되지 않았는데 이런 식으로 실험을 마치고 결론을 내리면 통계적 유의성에 심각한 영향을 줄 수 있다. 문제는 우연히 실험 초기에 p-value가 낮아질 수 있다는 점이다. 이를 믿고 실험을 종료하면 실제로는 없는 효과를 있다고 판단할 오류에 빠진다.
일단 적절한 실험 규모를 계산했다면 실험이 끝날 때까지 기다리는 것이 중요하다. 섣불리 결론을 내리고 의사 결정을 내리는 것은 위험하다.
현실적인 문제
이론적으로는 검정력과 유의 수준을 미리 정하고, 탐지하고자 원하는 효과 크기도 미리 알아서 실험 규모를 결정해야 한다. 가장 좋은 방법은 이 원칙을 따르는 것이지만, 실제로 이를 실무에서 행하기는 쉽지 않다. 특히 탐지하고자 원하는 효과 크기를 미리 가늠하는 것은 쉽지 않다. 결과적으로 실험 규모를 미리 정하는 것이 실무에서는 어려울 수 있다.
A/B 테스트는 표본 크기만으로 실험 지속 여부를 결정할 수 없는 경우도 있다. 예를 들어 주말과 주중의 고객 행동이 크게 다르다면, 아무리 많은 표본 크기를 얻었더라도 최소한 1주일 주기의 실험을 계획하는 것이 바람직하다.
전통적인 실험 방법은 변하는 세상에 대응하기 어렵다는 것도 문제다. 아무리 완벽한 무작위 실험을 하더라도 그 실험 결과는 과거의 것이다. 앞으로 고객이 같은 행동을 할 것이라는 전제가 성립하지 않으면 과거의 실험 결과로 미래의 의사 결정을 할 수는 없다.
이에 대한 대안으로 여러 가지 방법들이 있는데, 추후 다른 글에서 다루도록 한다.
결론
p-value는 통계적 실험에서 중요한 개념이 맞지만, 이것에만 휘둘려서는 안된다. 특히 A/B 테스트는 함께 고려할 요소가 많다. 유의 수준과 검정력, 탐지하고자 원하는 효과 크기를 정하고 이를 토대로 적정 실험 규모를 정해야 한다. 필요 이상으로 실험 규모를 키워서 과한(overpowered) 실험을 하는 것은 자원 낭비고 잘못된 의사 결정을 이끌 수 있다. 반대로 실험을 자꾸 엿보다가 부족한(underpowered) 실험을 하는 것은 오류에 빠질 가능성을 높인다. 현실적인 상황을 고려한 실험 운영도 필요한데, 전형적인 통계 실험 외의 대안을 찾아볼 필요도 있다.
실험 결과의 중요성을 한 번에 판단해 줄 마술 지팡이 같은 통계적 개념은 없다. p-value는 통계적 유의성 확보를 위한 도구이지, 실험 결과의 중요성을 평가하는 지표가 아니다. 실험 결과가 현실적으로 어떤 중요성을 갖는지 판단해야 한다. 그 결과를 얼마나 믿을 수 있는지는 그 다음 문제다.
참고
- The Essential Guide to Effect Sizes: Statistical Power, Meta-Analysis, and the Interpretation of Research Results
- How Not To Run An A/B Test
- Is Bayesian A/B Testing Immune to Peeking? Not Exactly
- A/B Testing Tech Note: determining sample size
- Is it possible to calculate the power of study retrospectively?
- The Use of Predicted Confidence Intervals When Planning Experiments and the Misuse of Power When Interpreting Results
- Simple Sequential A/B Testing
- Formulas for Bayesian A/B Testing
