웹 사이트 재방문 고객을 식별하기 위해서 인터넷 브라우저 쿠키에 고유한 키(key)를 삽입한다. 다른 고객과 겹치지 않는 키를 발급하려면 키의 길이가 길수록 유리하지만, 필요 이상으로 키가 길어지면 낭비다. 서로 다른 고객의 키가 겹칠 가능성을 계산하고, 적당한 키 길이를 고민해본다.

유니크 아이디

불특정 고객이 웹 사이트를 방문하면 해당 브라우저 쿠키에 고유 키를 발급해 추적한다. 같은 브라우저를 사용하여 고객이 다시 방문하면, 이전에 발급한 키를 조회하여 재방문 여부를 판별하고, 이전 활동을 조회하여 대처한다. 가능하다면 해당 유저에 특화된 컨텐츠를 웹 사이트가 제공하도록 조작한다.

이를 위해서 신규 방문 고객에게는 신규 키를 발급해야 한다. 고유 식별자(UUID)를 발급하는데는 여러 가지 방법이 있지만, 예시를 위해서 아주 간단한 키 발급 함수를 만든다.

# python3
from string import ascii_letters, digits
import random

def make_key(l):
    letters = ascii_letters + digits
    key = ''
    for _ in range(l):
        key += random.choice(letters)
    return key

알파벳 대소문자 52개와 숫자 10개, 총 62개 글자 중에서 $l$개를 무작위로 복원 추출하면 간단한 키를 만들 수 있다.

>>> random.seed(0)
>>> make_key(4)
'2yW4'
>>> make_key(8)
'Acq9GFz6'
>>> make_key(16)
'Y1t9EwL56nGisiWg'
>>> make_key(32)
'NZq6ITZM5jtgUe52RvEJgwBuNO6n9JEC'

키 길이는 길수록 좋다. 얼마나 길면 될까?

서로 다른 키의 개수

62개의 글자에서 무작위로 4개를 뽑아서 만든 문자열의 경우의 수는 14,776,336(=${62}^{4}$)개다. 길이가 4개인 키를 발급하면 이론적으로 약 천오백만 개의 서로 다른 키를 만들어낼 수 있다. 따라서 같은 키를 발급할 확률은 약 0.00000677%(=$ 1 / 14776336$)가 된다.

같은 키를 발급할 확률이 거의 0에 가깝다. 따라서 아주 짧은 길이의 키만으로도 충분할 것 같다. 그러나 단순히 같은 키를 발급할 확률만으로는 적당한 키의 길이를 정할 수 없다. 중요한 것은 서로 다른 고객이 같은 키를 발급받아서 같은 고객으로 오인될 가능성이다. 키를 발급받을 고객을 포함해서 확률을 계산해보자.

같은 키를 발급받은 고객이 존재할 확률

문제를 더 단순화시켜서 발급 가능한 모든 키의 개수가 365개라고 가정하자. 신규 고객이 방문하면 1부터 365사이의 자연수를 무작위로 발급한다.

2명의 신규 고객

신규 고객이 2명이라면 첫번재 고객은 365개의 키 중에서 하나를 발급받을 수 있다. 두번째 고객도 365개의 키 중에서 하나를 발급받는다. 이를 순서쌍으로 나타내면 아래와 같다.

(1, 1), (1, 2), (1, 3), ..., (1, 365),
(2, 1), (2, 2), (2, 3), ..., (2, 365),
(3, 1), (3, 2), (3, 3), ..., (3, 365),
...
(365, 1), (365, 2), (365, 3), ..., (365, 365)

가능한 순서쌍의 수는 133,225(=${365}^{2}$)개다. 이 중에서 같은 키를 갖는 경우는 아래와 같이 365개다.

(1, 1), (2, 2), (3, 3), ..., (365, 365)

따라서 2명의 신규 고객이 방문하고 365개의 키를 발급한다면, 같은 키를 발급받은 고객이 존재할 확률은

가 된다.

위의 확률은 여사건(complementary event)으로 계산할 수도 있는데, 고객이 3명 이상일 때 유용하다. 2명의 고객이 같은 키를 갖는 사건의 여사건은 서로 다른 키를 갖는 사건이다. 첫 번째 고객이 먼저 어떤 키를 발급받든지 상관없이, 두번째 신규 고객이 그것과 다른 키를 받으면 되므로 경우의 수는 132,860(=$365\times364)$다. 따라서 서로 다른 키를 발급 받을 확률은 아래와 같다.

여사건의 확률을 구했으므로, 다시 서로 같은 키를 받을 확률을 계산하면 아래와 같다.

k명의 신규 고객

위의 문제를 일반화시켜서 k명의 신규 고객이 방문하고 365개의 키를 발급하는 경우를 생각해보자.

알고 싶은 것은 k명의 신규 고객이 발급 받은 키 중에서 중복이 최소한 하나 이상 발견될 확률이다. 확률을 바로 계산하기 어려우므로 여사건을 이용한다. 관심 있는 사건에 대한 여사건은 k명 모두가 서로 다른 키를 발급 받는 사건이다. 신규 고객이 2명일 때와 마찬가지로 계산하면, 모든 신규 고객은 직전 신규 고객이 발급 받은 키와 다른 키를 발급 받으면 된다.

따라서 k명 모두가 서로 다른 키를 발급 받을 확률은 아래와 같다.

위의 여사건 확률을 이용해서, 같은 키를 받은 고객이 존재할 확률을 구하면 아래와 같다.

생일 문제

생일 문제(birthday problem)란 k명이 모였을 때, 생일이 같은 사람이 있을 확률을 계산하는 문제다. 이 문제는 k명에게 365개의 키를 발급하는 상황과 정확하게 같다.

언뜻 생각하면 생일이 같은 사람이 모이기 어려울 것 같지만, 23명만 모이면 생일이 같은 사람이 있을 확률은 50%를 넘는다.

50명이 모이면 생일이 같은 사람이 있을 확률은 약 97%가 된다.

# python3
from math import factorial

def prob_birthday(k, n=365):
    return 1 - factorial(n) / factorial(n - k) / (n**k)

>>> prob_birthday(23)
0.5072972343239854
>>> prob_birthday(50)
0.9703735795779884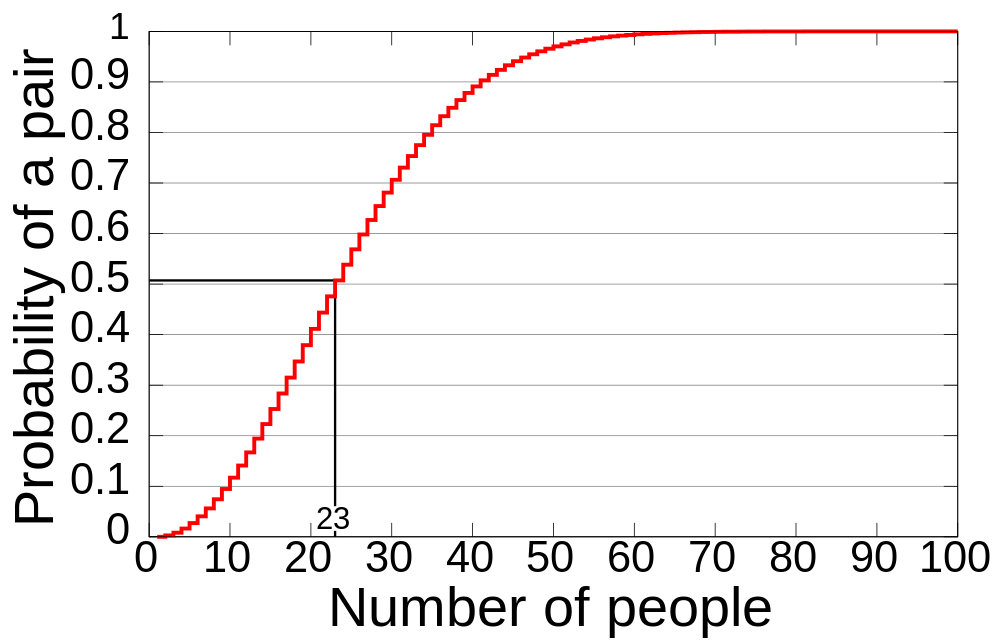

<같은 생일을 갖는 사람이 있을 확률 (출처: wikipedia)>

따라서 50명의 신규 고객에게 365개의 키는 부족하다.

적당한 키의 길이

생일 문제에서는 가능한 생일이 365개로 고정되어 있지만, 키 발급 문제에서는 키의 개수를 조정할 수 있다. 365로 고정되어 있었던 값을 n으로 일반화시키면 아래와 같은 식을 얻을 수 있다.

문제는 값이 커지면 계승(factorial) 계산이 어렵다는 점이다. 아래처럼 ‘OverflowError’가 발생한다.

>>> prob_birthday(200)
Traceback (most recent call last):
  File "<input>", line 1, in <module>
  File "<input>", line 2, in prob_birthday
OverflowError: integer division result too large for a float

계승 계산을 잘 하려고 노력하기 보다는 근사값을 사용한다. (참고: wikipedia)

62개의 글자에서 무작위로 4개를 뽑아서 만든 문자열의 경우의 수는 약 천오백만 (${62}^{4}=14776336$)개다. 만약 웹 사이트에 만 명의 신규 고객이 방문한다면 같은 키를 갖는 서로 다른 유저가 발생할 확률은 약 97%다. 키가 턱없이 짧다.

# python3
from math import exp

def approx_prob_birthday(k, n=365):
    return 1 - exp(-k**2 / (2 * n))

>>> 62**4
14776336
>>> approx_prob_birthday(10000, 62**4)
0.9660812995934986

천만 명의 신규 고객이 방문한다면, 키의 길이를 더 늘려야 한다. 키 길이를 8개로 늘리면 키의 개수는 $62^{8}$, 약 218조 개다. 그래도 같은 키를 갖는 서로 다른 고객이 생길 확률은 약 20%나 된다.

>>> 62**8
218340105584896
>>> approx_prob_birthday(10000000, 62**8)
0.20467188838610273

약 오천만 명의 신규 고객이 2개 이상의 다른 브라우저를 사용한다면 약 일억 번의 신규 방문이 가능하다. 키의 길이를 10개로 늘려서 계산해보면 키의 개수는 $62^{10}$, 약 팔경 사천조 개다. 같은 키를 발급받는 서로 다른 유저가 생길 확률은 약 0.6%다.

>>> 62**10
839299365868340224
>>> approx_prob_birthday(100000000, 62**10)
0.005939640084313247

일억 번의 신규 키를 발급할 예정이라면 최소한 10자리의 키를 발급하는 것이 좋다.

비트(bit) 단위의 키

알파벳 대소문자 52개와 숫자 10개만으로 키를 만드는 것은 낭비다. 보통 한 글자를 저장하는데 8비트, 즉 0 또는 1을 8개 사용하므로 $2^{8}$, 256개의 서로 다른 패턴을 만들 수 있다. 256개의 서로 다른 패턴을 만들 수 있는 공간을 사용하면서 62개의 문자로만 키를 구성하는 것은 나머지 194(= 256 - 62)개 패턴을 버리는 것과 같다.

62개 문자로 4자리 키를 만들면, 약 천오백만 개의 패턴을 만들 수 있었다. 실제로 4자리 키를 만드는데 사용하는 비트는 32(=$4\times8$)개이므로, 공간을 모두 활용하면 약 43억(=$2^{32}$) 개의 패턴을 만들 수 있다. 같은 공간을 사용하면서 훨씬 많은 패턴을 활용할 수 있다.

62개의 문자로 10자리 키를 만들면 총 80비트를 사용하는데, 비트 단위 키를 만들면 훨씬 적은 비트를 사용할 수 있다. 1억 번의 신규 발급에 64비트 길이의 키를 사용하면 키가 겹칠 확률은 약 0.03%다.

>>> approx_prob_birthday(100000000, 2**64)
0.00027101381224159393

생일 공격

생일 공격(birthday attack)이란 생일 문제의 확률적 특성을 이용한 암호 공격이다. 생일 문제(birthday problem)를 보면, 생각보다 적은 수의 사람이 모여도 생일이 같은 사람을 찾을 확률이 꽤 높다. 마찬가지로 생각보다 적은 시도 횟수로 해시 충돌(hash collision)을 찾으려는 시도가 생일 공격이다.

겹치지 않는 키를 발급하려는 시도와 생일 공격을 방어하려는 시도가 거의 같기 때문에 이를 참고하면 유용하다.

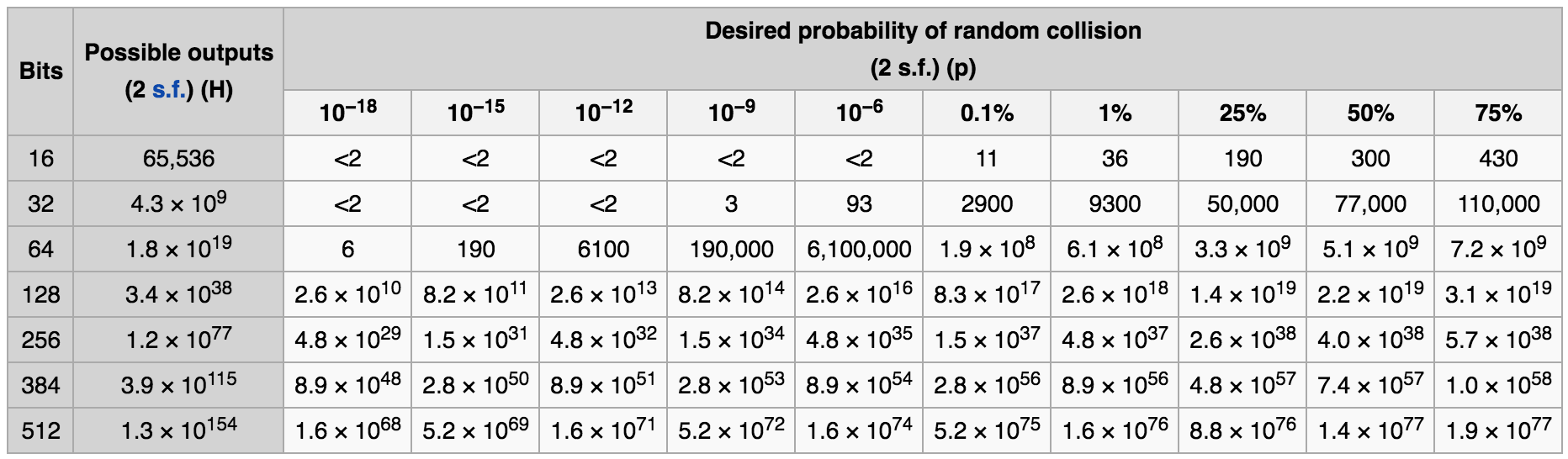<몇 개의 키를 발급하면 키가 겹치나? 출처: wikipedia>

위의 표는 키 길이와 키 충돌 확률에 따른 키 발급 수를 계산한 값이다. 예를 들어, 16비트 키를 만들면 총 65,536개의 서로 다른 키를 발급할 수 있고, 300개를 신규 발급하면 키가 겹칠 확률이 약 50%라는 것을 알 수 있다.

>>> approx_prob_birthday(300, 2**16)
0.4967385727487834

표를 참고하면 대략적인 상황에 맞춰서 키 길이를 결정하는데 도움이 된다. 브라우저 쿠키에 심을 유니크 키라면 64비트 정도로도 충분한 것으로 보인다.

결론

위의 문제는 실제로 개발을 하면서 마주친 문제였는데, 짝 프로그래머와 함께 의사결정을 내리는데는 약 5분 정도 걸렸다. 생일 문제(birthday problem)와 연관되어 있다는 점을 깨닫고 나서 문제가 아주 쉬워졌다. 개발을 하면서 마주치는 작은 문제들 중 상당 수는 간단한 통계 이론과 연관이 있다. 이런 부분을 그냥 지나치지 않고 고민하는 과정을 짧게라도 갖는 것이 참 유용하다.

5분이 지나도 결론을 내리지 못했다면, 아마도 그냥 충분히(?) 긴 키를 발급하고 넘어갔을 것이다. 현실에서도 큰 문제는 발생하지 않았을 것이다. 그러나 고민을 한 덕분에 기존에 알던 이론을 현실에 적용해볼 수 있고, 그만큼 더 알 수 있다. 그래서 더 재미있다.