박스 플롯(box plot) 또는 박스앤위스커 플롯(상자수염플롯; box-and-whisker plot)은 데이터의 대략적인 분포와 개별적인 이상치들을 동시에 보여줄 수 있으며 서로 다른 데이터 뭉치를 쉽게 비교할 수 있도록 도와주는 시각화 기법으로 가장 널리 쓰이는 시각화 형태 중 하나이다.

통계학자 존 튜키(John Tukey)가 1977년 저서 “탐색적 데이터 분석(Exploratory Data Analysis)”에서 처음 제시한 것으로 알려져 있으나, 매리 엘리너 스피어Mary Eleanor Spear가 1952년에 저서 <Charting Statistics>에서 “범위 막대(range bar)”라는 이름으로 먼저 제안한 바 있다. 범위 막대에서는 수염의 양 끝이 최대값과 최소값을 나타내고, 상자는 사분위수범위를 나타내며, 상자 안에 중앙값을 표현하는 방식으로 “5가지 요약 수치”를 표현한다. 튜키에 비해 25년 앞서 거의 동일한 형태를 제안하였으나 상대적으로 잘 알려져 있지 않다.

박스 플롯은 널리 쓰이는 만큼이나 다양한 변형이 존재하기도 하고 정확하게 이해하지 않은 채로 쓰이는 경우가 종종 있다. 이 글에서는 박스플롯이 어떻게 그려지는지, 왜 그렇게 그려지게 되었는지, 어떤 의미들을 읽어낼 수 있는지 등을 살펴보겠다.

사분위수와 5가지 요약 수치

여러 액체의 어는점을 측정한 한 뭉치의 데이터를 구했다고 치자. 데이터가 적다면 모든 값들을 눈으로 훑어볼 수도 있겠지만, 그렇지 않다면 이해할 수 있는 수준으로 요약해서 보는 편이 나을 것이다. 데이터에 담겨 있는 일반적인 값들이 대략 어떠한지를 요약해서 보고, 예외적인 값들만 따로 본다면 데이터의 양이 많더라도 비교적 쉽게 파악할 수 있다.

상당히 많은 경우에 데이터들이 특정 값 언저리에 모여있는 편인데(이를 “모드”가 하나라는 의미에서 “unimodal”이라고 부른다) 이 중심에 해당하는 값을 알면, 즉 액체들이 대체로 몇 도 언저리에서 어는지를 알면 유익할 것이다. 이를 중심경향성이라고 한다. 중심경향성을 알려주는 가장 널리 쓰이는 통계량은 산술 평균(mean)이다. 하지만 이 값은 데이터에 극단적으로 크거나 작은 값이 섞여 있으면 영향을 많이 받는 단점이 있다. 강건성(robustness)이 낮다고 말한다.

강건성이 높으면서 중심경향성을 알려주는 통계량으로는 사분위수 중 제2사분위수가 있다. 사분위수란 데이터에 속한 값들을 작은 값부터 큰 값 순으로 줄 세운 뒤에 이들을 네 조각으로 나누는 세 개 지점(막대기를 4등분 하려면 3개의 지점이 필요하다)에 해당하는 수들을 말한다. 제2사분위수는 세 개 값 중 두번째 값을 뜻하므로 정확히 중앙에 있는 값이라 하여 다른 말로 중앙값(median)이라고도 부른다.

아래 그림에서 극단적으로 큰 값이 추가되었을 때 중앙값(제2사분위수; Q2)은 거의 변하지 않지만 산술 평균은 상당히 우측으로 이동하는 현상을 볼 수 있다. 중앙값은 강건성이 높지만 산술 평균은 강건성이 낮기 때문이다.

중심부를 알아낸 뒤에는 중심부 언저리에 값들이 얼마나 오밀조밀 모여있는지 혹은 넓게 퍼져있는지(퍼짐정도)도 함께 알면 유용할 것이다. 보통은 표준편차를 쓰지만 이 값도 강건성이 낮기 때문에 1사분위수(데이터의 25% 지점)와 3사분위수(데이터의 75% 지점) 사이의 간격을 나타내는 사분위수범위(IQR; inter-quartile range = Q3 - Q1)를 쓰곤 한다.

데이터 안에 담긴 값들 중 절반은 Q1와 Q3 범위 안에 있고 그 중에서도 값들이 가장 많이 몰린 지점은 Q2이므로 이 세 가지 값만 알면 데이터 안에 서로 상대적으로 비슷한 값들이 많이 모인 큰 뭉텅이를 비교적 잘 요약할 수 있다.

이제 단 세 개의 통계량(Q1, Q2, Q3)으로 데이터 안에 담긴 일반적인 값들을 요약했으므로 특이한 값들을 살펴볼 차례다. 데이터의 최소값과 최대값을 보면 이 목적을 어느 정도 달성할 수 있다.

이 다섯가지 통계량, 즉 최소값, 제1사분위수, 제2사분위수, 제3사분위수, 최대값을 ‘5가지 요약 수치(five-number summary)’라고 부른다. 최소값과 최대값은 강건성이 낮지만 양쪽 끝에 있는 값(즉, 가장 극단적인 값들)을 정확히 알려준다는 점에서 유익하다. 제1사분위수, 제2사분위수, 제3사분위수는 강건성이 높고 데이터의 상당 부분을 요약하여 보여주므로 유익하다.

박스플롯은 5가지 요약 수치를 잘 보여주는 시각화 기법으로, 가장 널리 쓰이는 형태는 두 종류가 있다.

시각화 방법 1

박스 플롯의 상자는 제1사분위수(Q1), 제2사분위수(Q2), 제3사분위수(Q3)를 드러낸다. 상자의 좌측 변과 우측 변은 각각 Q1과 Q3의 위치를 나타낸다. 따라서 상자의 길이는 전체 데이터의 정확히 절반이 담겨 있는 범위인 사분위수범위를 시각적으로 표현한다. 상자 안의 눈금은 Q2(즉, 중앙값)를 보여준다.

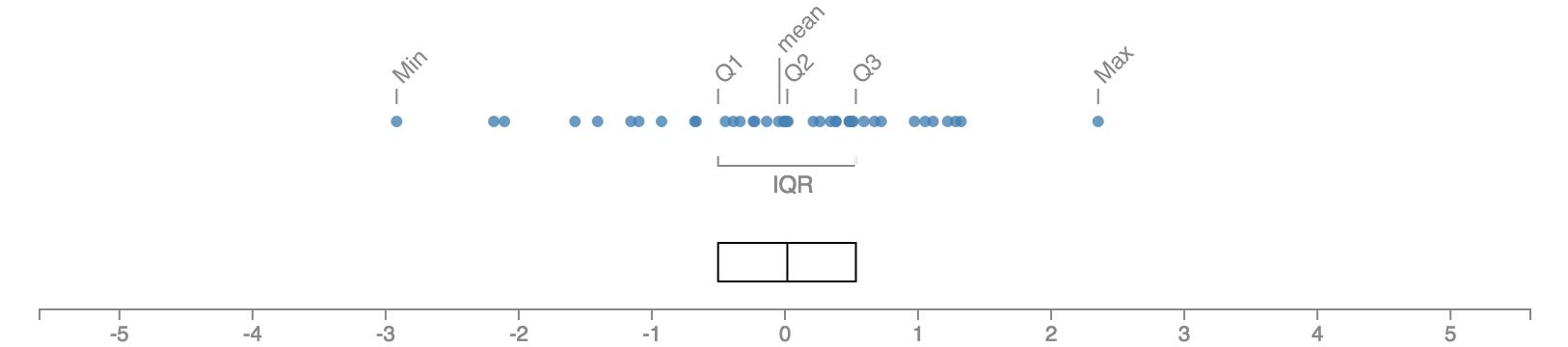
이 상태에서 최소값과 최대값 위치까지 수염(whisker)을 그려주면 위에서 설명한 5가지 요약 수치를 보여주는 박스 플롯이 만들어진다. 하지만 튜키는 이 방법을 설명한 직후에 조금 더 복잡하지만 유용한 다른 방식을 제안한다.

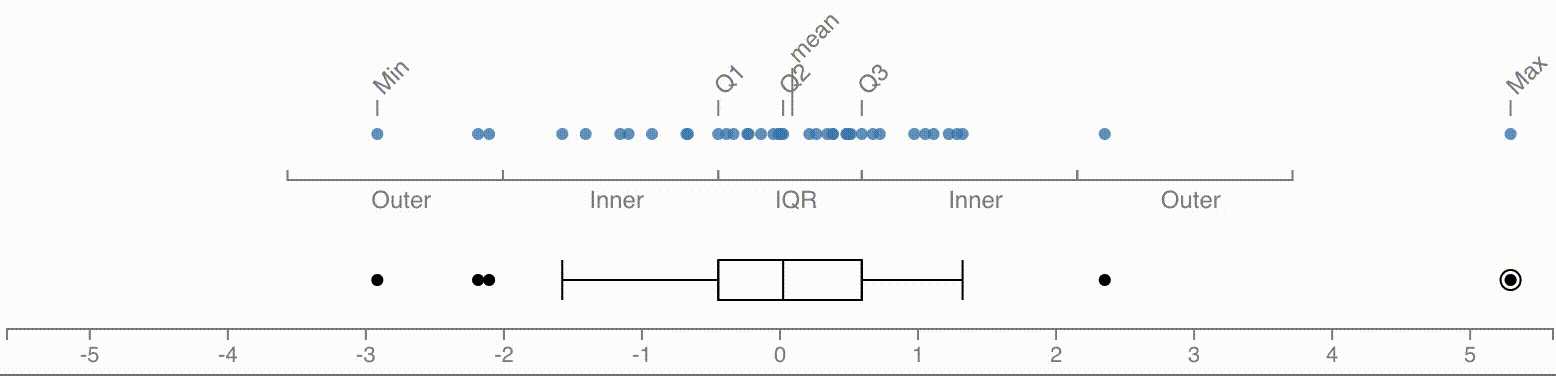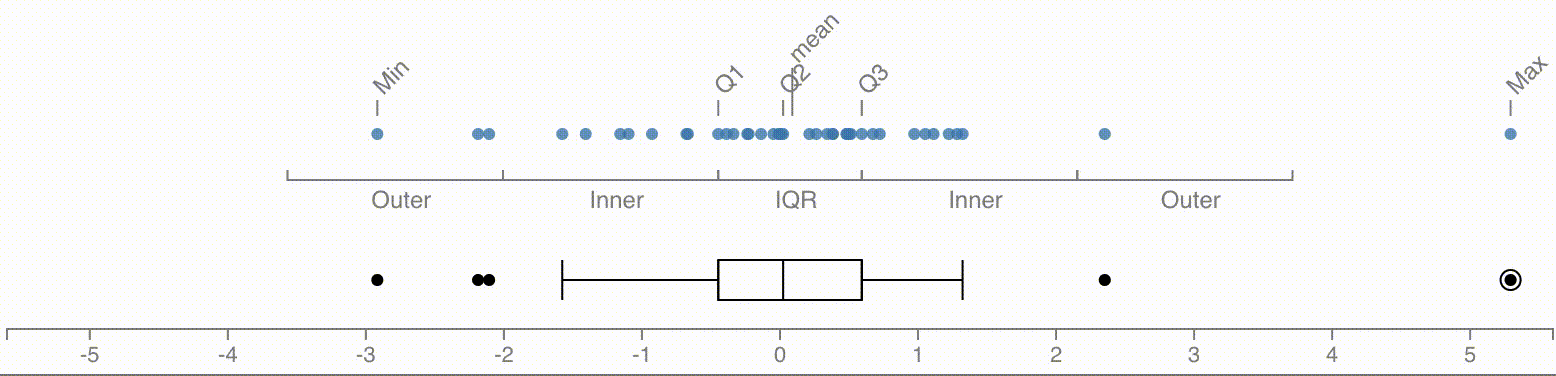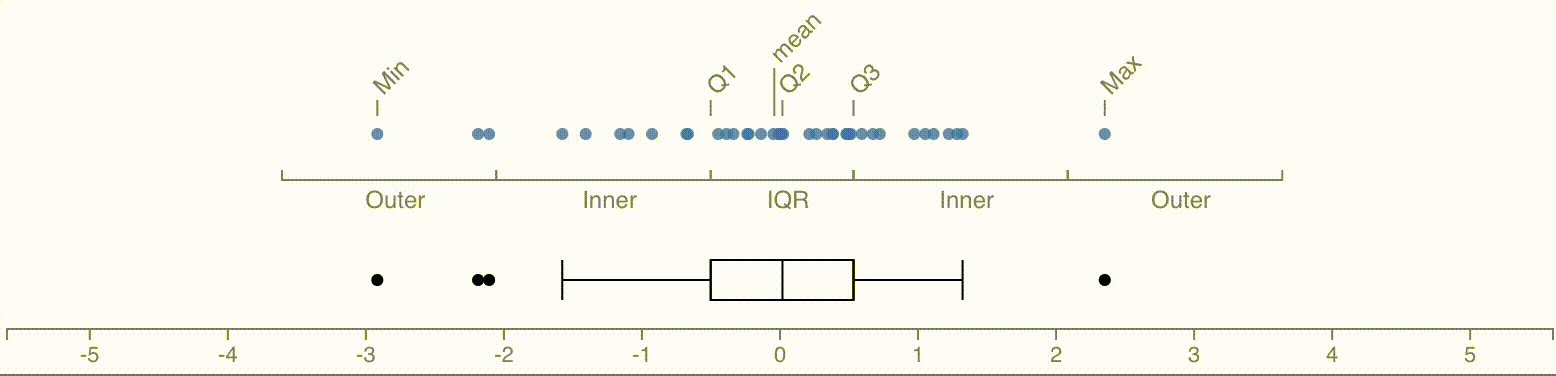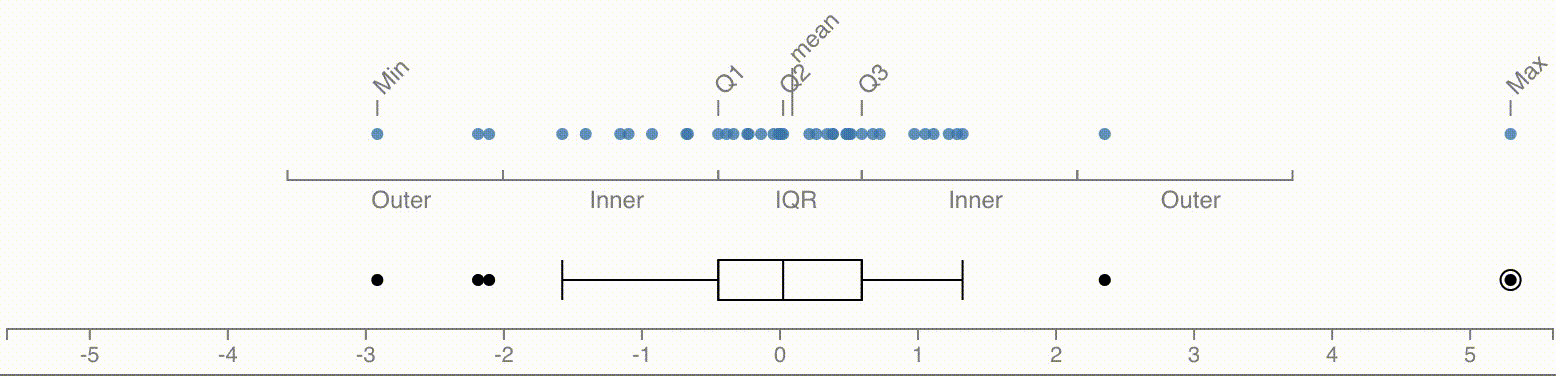
시각화 방법 2: 스키매틱 플롯

이번에 설명할 형태는 스키매틱 플롯 또는 튜키 박스 플롯이라고 불리며, 가장 널리 쓰이는 형태이다. 한편 잘못된 방법으로 표현되는 경우도 많고 읽는 방법에 대해 잘못 설명하는 책이나 글도 많으므로 주의가 필요하다.

상자 길이의 1.5배에 해당하는 길이, 즉 1.5 IQR을 한 걸음(step)이라고 부른다. 상자의 양 끝에서부터 한걸음씩 떨어진 지점 사이의 공간을 안쪽 울타리(inner fence)라 부르고 안쪽 울타리 끝에서부터 한걸음씩 더 떨어진 지점 사이의 공간을 바깥쪽 울타리(outer fence)라 부른다.

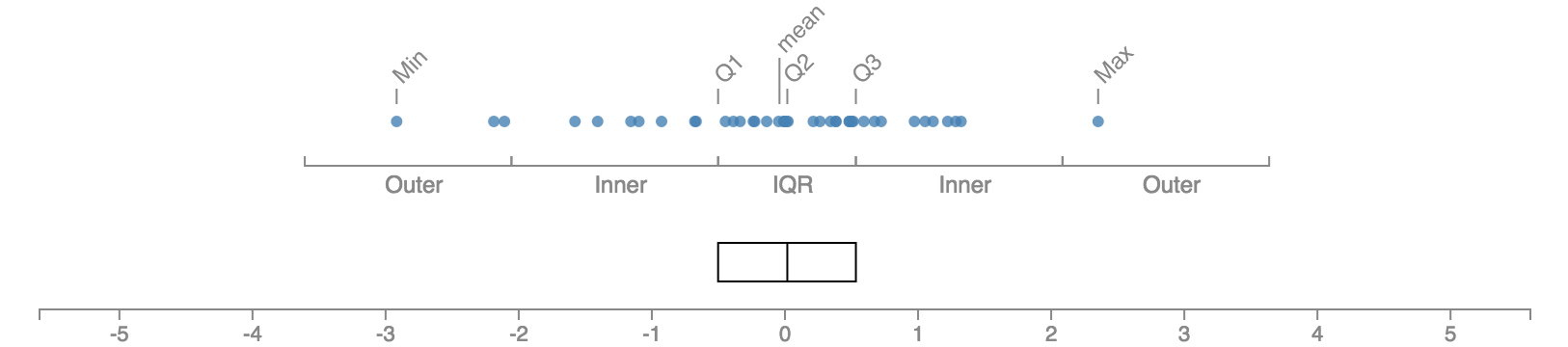
스키매틱 플롯에서는 최소값과 최대값까지 수염을 그리는 대신, 안쪽 울타리 내의 데이터 중에서 가장 상자로부터 멀리 떨어진 데이터가 있는 지점까지만 수염을 그린다.

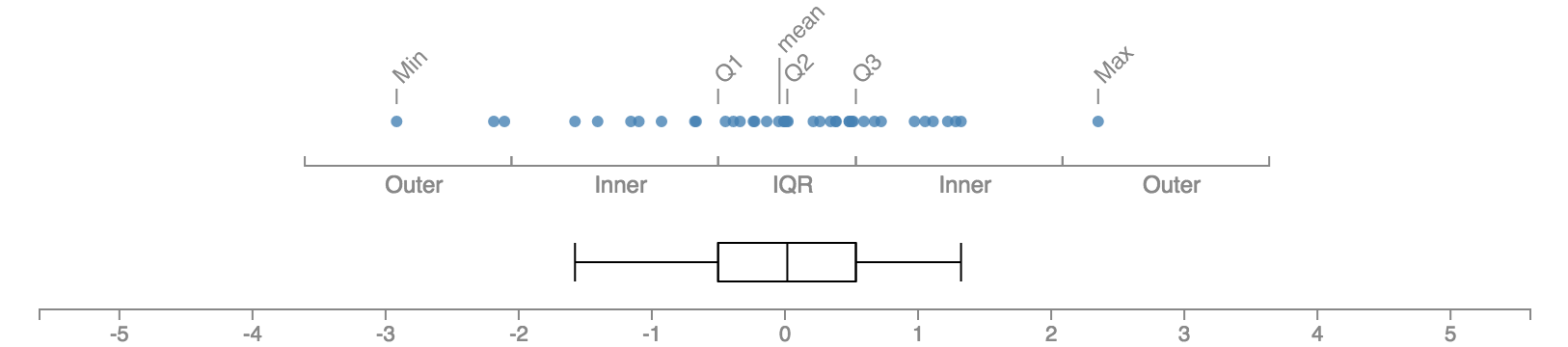
몇몇 책에서는 안쪽 울타리와 바깥쪽 울타리의 경계 지점까지 수염을 그리는 것이라고 설명하기도 하고 몇몇 시각화 프로그램은 실제로 그렇게 그리기도 하지만 이 방식은 좋지 않다. 예를 들어 2019년 2월 19일 기준으로 파이썬의 seaborn.boxplot() 및 pandas.DataFrame.boxplot()은 수염을 제대로 그려주지만, 자바스크립트의 vegalite는 잘못된 방식으로 그려준다. 다음 릴리즈인 3.0.0에서 고쳐질 예정이다.

튜키는 항상 두 가지를 중요하게 여겼는데, 하나는 일반적인 경향을 잘 요약하여 드러내는 것이고, 다른 하나는 일반적인 경향에서 벗어나는 특수한 데이터를 되도록 개별적으로 최대한 드러내는 것이다. 데이터의 절반이 몰려있는 부분은 상자로 요약하여 보여주되, 제법 떨어진 곳의 데이터가 정확히 어디에 있는지는 직접 드러내기 위해 수염은 항상 실제 데이터가 존재하는 위치에서 끝나도록 그리는 것이다. 튜키가 제시한 원칙에 따라 그려진 박스 플롯이라면 수염이 끝나는 위치에는 항상 실제 데이터가 있다. 수염을 데이터와 상관 없이 1.5 IQR까지 그리면 이 특성이 사라진다.

1.5 IQR을 벗어난 데이터, 즉 바깥쪽 울타리에 있는 데이터는 더욱 특수한 데이터이므로 개별 데이터를 모두 점으로 찍어서 나타낸다.

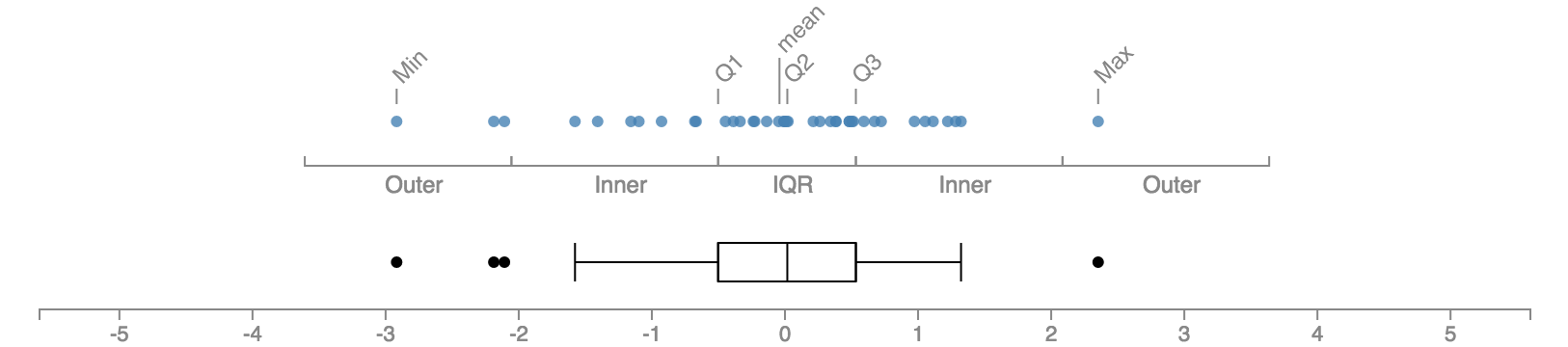
만약 바깥쪽 울타리보다 더 멀리에 있는 값이 있다면? 튜키는 이런 값들을 “far outs”라고 부르며 더 강하게 표시할 것을 권한다. 우리 데이터엔 이런 극단적인 값이 없으니 임의로 추가를 해서 그려보자.

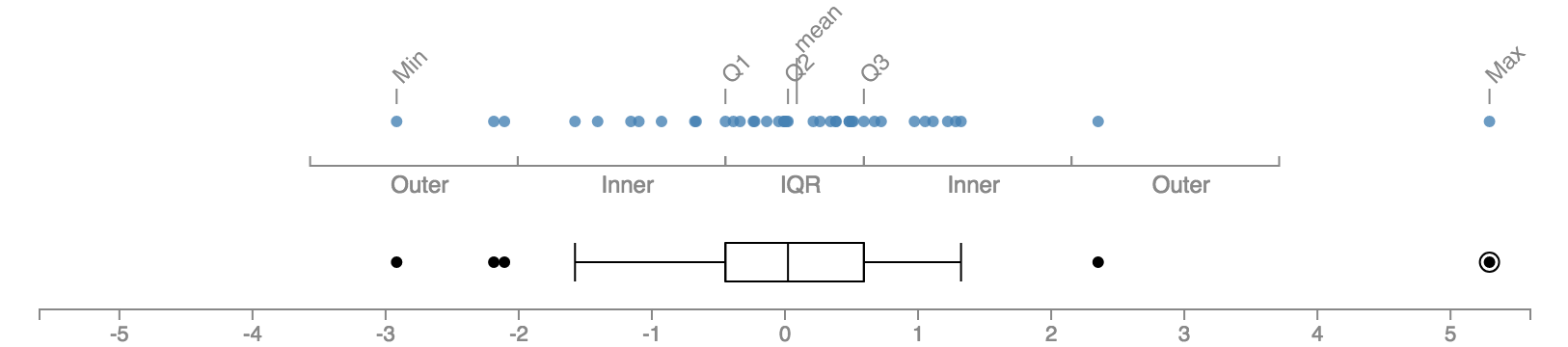
극단적 아웃라이어가 우측에 추가되었으나 상자의 크기, 중앙값의 위치, 수염의 길이 등은 거의 변하지 않았다는 점에 주목하기 바란다. 박스 플롯의 그래픽 요소, 특히 상자 부분은 높은 강건성을 갖는다. 그러면서도 동시에 예외적인 값들을 빠짐없이 표현해내고 있다.

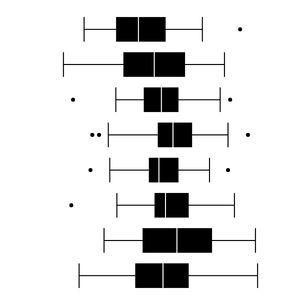
다양한 변형

스키매틱 플롯이 가장 널리 쓰이는 형태이며 보통 튜키 박스 플롯이라고 부르지만, 박스 플롯은 한 종류가 아니다. 수염의 길이가 최대값과 최소값까지 늘어나는 형태(앞에서 잠깐 설명한 바 있다), 그 밖에도 상자 부분을 시각적으로 극도로 단순화한 형태(Edward Tufte), 중앙값 주변을 오목하게 파서 여러 중앙값 사이에 통계적으로 유의미한 차이가 있는지 여부를 시각적으로 드러내는 형태(notched box plot) 등 다양한 변형이 있다.

이 중 튜키가 제안한 특정한 방식이 항상 가장 뛰어나다고 할 수는 없고 그 방식을 빠짐없이 그대로 따라야만 하는건 아니다. 심지어 이 글에서 설명한 형태도 엄밀히 따지면 튜키의 제안에서 벗어난 지점들이 있다. 예를 들어 스키매틱 플롯을 그리는 경우에 수염은 반드시 점선으로 표현해야 한다. 이상치들에는 점만 찍는 것이 아니라 개별 데이터의 레이블도 소문자로 적어주어야 한다. 극단적 이상치는 X로 표시하고 대문자로 레이블을 적어야 한다.

몇 가지 변형을 살펴보자.

박스 플롯을 좁은 간격으로 나란히 그리면 여러 데이터 뭉치를 쉽게 비교할 수 있다.

상황에 따라 세로로 그릴 수도 있다.

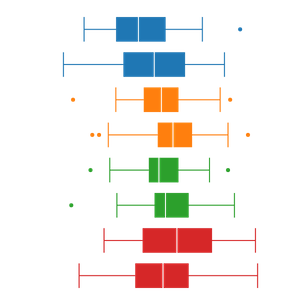
데이터 뭉치 사이에 관련성이 있다면 같은 색상을 써서 시각적으로 짝지어주면 좋다. 데이터 뭉치 사이에 어떠한 순서(order)가 있는게 아니라면 명도나 채도 차이를 보다는 색조(hue) 차이를 주어야 불필요한 오해를 줄일 수 있다.

박스 플롯 위에 스트립 플롯을 겹친 형태로 그려서 개별 데이터의 분포를 직접 드러낼 수도 있다.

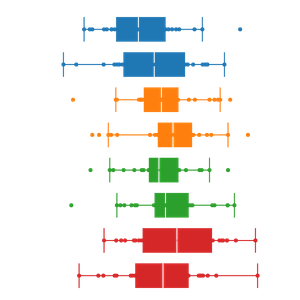
이 경우, 데이터가 지나치게 많거나 서로 겹쳐 있으면 어디에 데이터가 얼마나 몰려 있는지 시각적으로 알기가 어렵기 때문에 점의 위치를 아주 조금 흩뿌려주면 좋다. 이를 지터링(jiterring)이라고 한다. 상자와 점이 겹쳐 있어서 잘 보이지 않는다면 투명도를 약하게 적용해도 좋다.

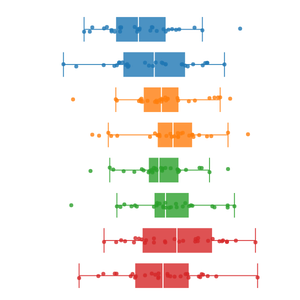
다만 항상 많은 데이터를 시각적으로 담아내는 것이 좋은 시각화인 것은 아니다. 박스 플롯의 장점은 간소한 형태만으로 데이터에 대해 많은 것을 이야기해준다는 점에 있다. 그런 의미에서 더 단순화할 방법을 생각해보는 것도 유용하다. 예를 믈어 에드워드 터프티가 제안한 최소주의 형태로 나타내도 데이터가 시각적으로 잘 드러난다면 이 형태를 쓰는 것도 좋다.

다만 이 경우엔 다시 투명도를 제거하여 색상 차이가 더 잘 드러나게 해주어야 한다. 면적이 좁아지면 색상의 차이를 지각하기가 더 어려워지기 때문이다.

아래와 같이 산포도(scatter plot)의 각 축에 박스 플롯을 그리는 변형도 고려해볼만 하다.

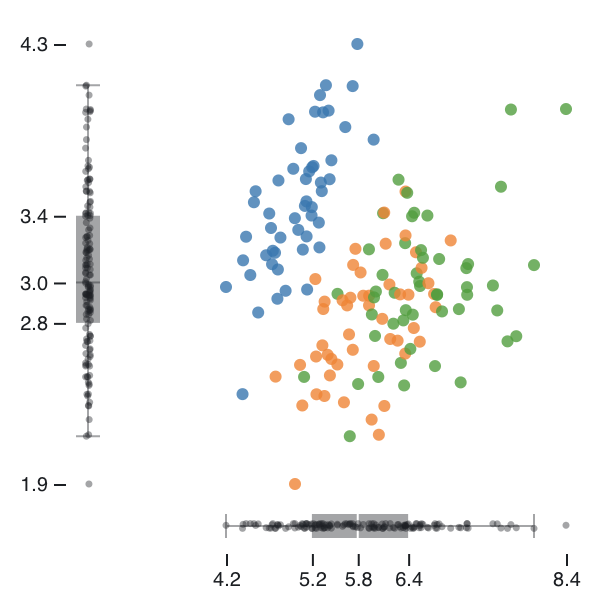
산포도는 두 변수 사이의 상관 관계를 잘 드러내지만 각 변수의 분포를 따로 보기는 어렵다는 단점이 있다. 산포도의 각 축을 박스 플롯으로 대체하면 별도로 공간을 거의 차지하지 않으면서도 개별 변수의 분포를 함께 보여줄 수 있어서 좋다. 위 그림에서는 각 축이 5가지 요약 수치도 명시적으로 보여주고 있다.

맺음말

수염이 끝나는 위치에 대한 제안은 어떻게 하면 중요한 데이터를 잘 드러낼 것인지에 대한 고민 끝에 내려진 것이며 현재에도 여전히 의미가 있다. 반면 강조 표시를 X표로 해야 한다거나 대문자로 해야 한다는 식의 제안은 종이와 팬으로 수작업을 하던 당시의 상황을 염두에 둔 제안이므로 현재에는 다소 달리 해석할 여지가 있다. 이와 같이 어떠한 지혜가 어떤 맥락에서 어떤 고민을 거쳐 얻어진 것인지를 잘 이해하기 위해 노력하면 이 지혜를 현재 내가 겪고 있는 상황 하에서 어떻게 변형하여 잘 활용할지에 대해서도 더 잘 생각해볼 수 있을 것이다.